��Ŀ����
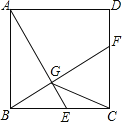
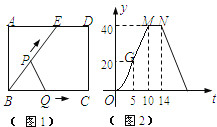
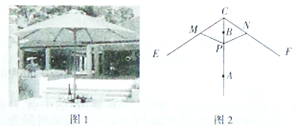
����Ŀ����ͼ1��ʾ������ɡ,ɡ����ֱ��ˮƽ����,��ʾ��ͼ��ͼ2��ʾ,��ɡ�ս�ʱP��A�غ�,��ɡ�����ſ�ʱ,����P��A��B�ƶ�,����P����Bʱ,ɡ�ŵ��,��ʱ����Žǡ�ECF=150��,��֪ɡ�ڳſ��Ĺ�����,����PM=PN=CM=CN=6.0����CE=CF=18.0����.
(1)��AP����ȡֵ��Χ;
(2)����CPN=60��,��AP��ֵ;
(3)�����ⴹֱ������,ɡ�ŵ��ʱ,��ɡ�µ���Ӱ(�ٶ�ΪԲ��)���S.(�������![]() )(�ο�����:sin75���0.97,cos75���0.26,tan75���3.73)
)(�����:sin75���0.97,cos75���0.26,tan75���3.73)
���𰸡���1��AP��ȡֵ��ΧΪ0��AP��8.88��������2��AP=6��������3��ɡ����Ӱ���Ϊ![]() ƽ������
ƽ������
�����������������
��1������ͼ������P���B�غ�ʱ��AP�����ʱ��MCN=150��������MN��BC�ڵ�O�����������ı���CMPN�����Σ��������ζԽ����ഹֱƽ�ֿɵá�COM=75�㣬���CM=6.0���ף��ɽ��CO=1.56�������Ӷ��ɵ�BC=3.12���ף��ٽ��AC=12���ɵ�AB=8.88�������ɴ˼��ɵõ�![]() ��
��
��2������CPN=60��ʱ�����PN=CN=6����֪��CPN��ʱ�ǵȱ������Σ���CP=6�����AC=12�ɵô�ʱAP=6���ף�
��3������ͼ���������֪����ʱ��P��B�غϣ�����EF��AC�ڵ�D���ɣ�1����֪MO=MC��sin��MCO=5.82(����)���Ӷ��ɵ���MN=11.64(����)����֤��CMN�ס�CEF���ɽ����֪���EF�ij����Ӷ�����������������.
���������
(1)����P��B�غ�ʱ,AP�,
��ʱ��MCN=1500
��ͼ��ʾ������MN��CB�ڵ�O��
��PM=PN=CM=CN=6.0����,
���ı���CMPN�����Σ�
��CB��MN,����COM=90��,��MCO=![]() ��MCN=75����
��MCN=75����
��Rt��MCO��,��MCO=75��,CM=6.0����,

��CO=CM��cos��MCO=6.0��0.26=1.56(����)��
��BC=2C0=3.12(����)��
��AC=MC+MP=12(����),
��AP=12-3.12=8.88(����)��
��AP��ȡֵ��ΧΪ0��AP��8.88���ף�
(2)����CPN=60��ʱ,CP=CM=6����,
��AP=6���ף�
(3)ɡ�ſ����ʱ,��P��B�غ�,��ͼ��ʾ,����EF��AC��D��
��(1)�ɵ�MO=MC��sin��MCO=6.0��0.97=5.82(����)��
MN=2MO=11.64(����)��
����CMN����CEF��,��MCN=��ECF,CM=CN,CE=CF��
���CMN�ס�CEF��
![]() ��
��
��EF=34.92���ף�
��ɡ����Ӱ���![]() (ƽ������).
(ƽ������).

����Ŀ����ͼ�����ڸ��˵�ϰ�߲�ͬ��˫�ֽ���ʱ���ִ�Ĵָ�����ִ�Ĵָ������һ������¼�������ʦ�����ν̵�ѧ������һ�����飬ͳ�ƽ�����±���ʾ��
2011�� | 2012�� | 2013�� | 2014�� | 2015�� | |
����ʵ������� | 106 | 110 | 98 | 104 | 112 |
���ִ�Ĵָ���ϵ����� | 54 | 57 | 49 | 51 | 56 |
Ƶ�� | 0.509 | 0.518 | 0.500 | 0.490 | 0.500 |
���ݱ����е����ݣ�����Ϊ���������¼��У����ִ�Ĵָ���ϵĸ��ʿ��Թ���Ϊ��������

A. 0.6 B. 0.5 C. 0.45 D. 0.4