题目内容
【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一小题计分.
(1)方程x2﹣9x+18=0的两个根是等腰三角形的底和腰,则这个等腰三角形的周长为_____.
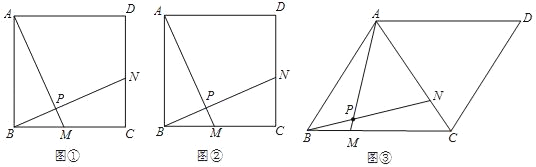
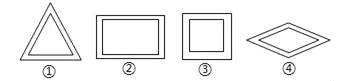
(2)如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应平行,且对应边之间的距离都相等,那么两个图形不相似的一组是(请填写正确答案的序号)_____.
【答案】15 ②.
【解析】
(1)解原方程可得方程的两根,![]() =3,
=3,![]() =6,根据三角形的性质“两边之和大于第三边, 两边之差小于第三边”,可得腰为6,底边长为3,可得周长;
=6,根据三角形的性质“两边之和大于第三边, 两边之差小于第三边”,可得腰为6,底边长为3,可得周长;
(2)根据图形相似要求对应角相等、对应边成比例可得答案.
解:(1)方程因式分解可得:(x-3)(x-6)=0,故原方程的解为![]() =3,
=3,![]() =6,
=6,
![]() 两个根是等腰三角形的底和腰, 根据构成三角形的条件“两边之和大于第三边, 两边之差小于第三边”,
两个根是等腰三角形的底和腰, 根据构成三角形的条件“两边之和大于第三边, 两边之差小于第三边”,
![]() 可得等腰三角形的腰为6, 底边长为3,
可得等腰三角形的腰为6, 底边长为3, ![]() 所以这个等腰三角形的周长为6+6+3=15,
所以这个等腰三角形的周长为6+6+3=15,
故本题正确答案为15.
(2)图形相似即要求对应角相等、对应边成比例,
等边三角形的三个内角都是60![]() ,三条边都相等,故①中的图形相似;
,三条边都相等,故①中的图形相似;
矩形的四个内角都是90![]() ,对边相等,所以对应边不一定成比例,故②中的图形不一定相似;
,对边相等,所以对应边不一定成比例,故②中的图形不一定相似;
正方形的四个内角都是90![]() ,四条边都相等,故③中的图形相似;
,四条边都相等,故③中的图形相似;
菱形的对角相等, 四条边都相等, 故④中的图形相似;
故答案为:②.

练习册系列答案
相关题目