题目内容
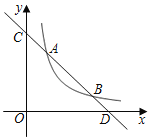
【题目】如图,已知一次函数y1=kx+b与反比例函数y2=![]() (x>0)的图象分别交于点A(2,4)和点B(4,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点A(2,4)和点B(4,n),与坐标轴分别交于点C和点D.
(1)求反比例函数和一次函数的解析式;
(2)求y1<y2时,自变量x的取值范围;
(3)若点P是x轴上一动点,当△ABP为直角三角形时,求点P的坐标.
【答案】(1)y2=![]() ,y1=﹣x+6;(2)0<x<2或x>4;(3)P点坐标为(﹣2,0)或(2,0).
,y1=﹣x+6;(2)0<x<2或x>4;(3)P点坐标为(﹣2,0)或(2,0).
【解析】
(1)先把A点坐标代入y2=![]() 中求出m得到反比例函数解析式为y2=
中求出m得到反比例函数解析式为y2=![]() ,再利用反比例函数解析式确定B点坐标,然后利用待定系数法求一次函数解析式;
,再利用反比例函数解析式确定B点坐标,然后利用待定系数法求一次函数解析式;
(2)在第一象限内,写出反比例函数图象在一次函数图象上方所对应的自变量的范围即可;
(3)设P(t,0),利用两点间的距离公式得到PA2=(t﹣2)2+42,PB2=(t﹣4)2+22,AB2=(4﹣2)2+(2﹣4)2,讨论:根据勾股定理,当∠PAB=90°时,t2﹣4t+20+8=t2﹣8t+20;当∠PBA=90°时,t2﹣8t+20+8=t2﹣4t+20;当∠APB=90°时,t2﹣4t+20+t2﹣8t+20=8,然后分别解关于t的方程可得到P点坐标.
解:(1)把A(2,4)代入y2=![]() 得m=2×4=8,
得m=2×4=8,
∴反比例函数解析式为y2=![]() ,
,
把B(4,n)代入y2=![]() 得4n=8,解得n=2,则B(4,2),
得4n=8,解得n=2,则B(4,2),
把A(2,4)和B(4,2)代入y1=kx+b得![]() ,
,
解得![]() ,
,
∴一次函数解析式为y1=﹣x+6;
(2)根据函数图象可得:当0<x<2或x>4时,y1<y2;
(3)设P(t,0),
∵A(2,4),B(4,2)
∴PA2=(t﹣2)2+42=t2﹣4t+20,PB2=(t﹣4)2+22=t2﹣8t+20,AB2=(4﹣2)2+(2﹣4)2=8,
当∠PAB=90°时,PA2+AB2=PB2,即t2﹣4t+20+8=t2﹣8t+20,解得t=﹣2,此时P点坐标为(﹣2,0),
当∠PBA=90°时,PB2+AB2=PA2,即t2﹣8t+20+8=t2﹣4t+20,解得t=2,此时P点坐标为(2,0),
当∠APB=90°时,PA2+PB2=AB2,即t2﹣4t+20+t2﹣8t+20=8,整理得t2﹣6t+16=0,方程没有实数解,
综上所述,P点坐标为(﹣2,0)或(2,0).

【题目】某微商销售的某商品每袋成本20元,设销售价格为x(单位:元/袋),该微商发现销售量y与销售价格x之间的关系如表:
销售价格x(元/袋) | 25 | 30 | 35 | 40 |
销售件数y | 275 | 250 | 225 | 200 |
(1)求y关于x的函数表达式;
(2)根据物价部门的规定,商品的利润率不能超过100%,该微商应该如何定价,才能使获得的利润最大,最大利润是多少?