题目内容
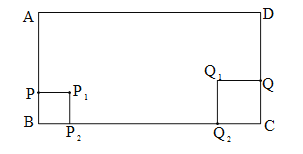
【题目】在长方形ABCD中，AB=a，BC=2a，点P在边BA上，点Q在边CD上，且BP=m，CQ=n，其中，m＜a，n＜a，m≠n，在长方形ABCD中，分别以BP、CQ为边作正方形BPP1P2，正方形CQQ1Q2（点P2、Q2在边BC上）．
（1）画出图形．
（2）当m＜n时，求三角形PQ1C的面积．
【答案】（1）答案见解析；（2）
．
【解析】
（1）根据题意画出图形即可；
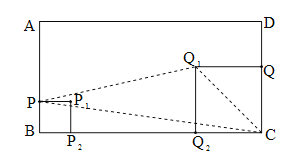
（2）连结PQ1，Q1C，PC．根据△PQ1C的面积=梯形PBQ2Q1面积+△Q1Q2C面积－△PBC面积计算即可．
（1）所画图形如下：
（2）如图，连结PQ1，Q1C，PC．则△PQ1C的面积=梯形PBQ2Q1面积+△Q1Q2C面积－△PBC面积=
=．
练习册系列答案
相关题目
【题目】光明奶粉每袋标准质量为454克，在质量检测中，超出标准质量2克，记为
克，低于标准质量2克，记为
克.若质量低于标准质量3克和3克以上，则这袋奶粉视为不合格产品，现抽取10袋样品进行质量检测，结果如下（单位：克）
袋号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
记作 |
| 0 | 1 |
|
|
|
|
|
|
|
（1）这10袋奶粉中，有哪几袋不合格？
（2）这10袋奶粉中质量最多的是哪袋？它的实际质量是多少？
（3）这10袋奶粉中质量最少的是哪袋？它的实际质量是多少？
（4）与标准质量比较，10袋奶粉总计超过或不足多少克？
