题目内容
【题目】如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM.
(1)求证:AP=CE;
(2)求∠PME的度数;
(3)求证:BM平分∠AME;
(4)AM,BM,MC之间有怎样的数量关系,直接写出,不需证明.

【答案】(1)见解析;(2)60゜;(3) 见解析;(4)AM+MC=BM
【解析】
(1)先证△APB≌△CEB,即而可得AP=CE,
(2)在△MCP和△∠BCE中,由三角形的内角和为180°,可得∠PME=∠PBE=60゜
(3)分别过点B作BN⊥AM于N,BF⊥ME于F,先证△BNP≌△BFE,可得BN=BF,由角平分线的判定可证BM平分∠AME.
(4)在BM上截取BK=CM,连接AK.可得△ACM≌△ABK,则AK=AM,所以AM+MC=BM.
证明:(1)在△APB和△CEB中
AB=BC,∠ABP=∠CBE,BP=BE,
∴△APB≌△CEB (SAS),
∴ AP=CE,
(2)∵△APB≌△CEB,
∴∠APB=∠CEB,
∵∠MCP=∠BCE,
则∠PME=∠PBE=60゜
(3)作BN⊥AM于N,BF⊥ME于F,
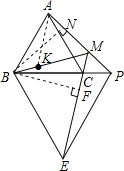
∵△APB≌△CEB,
∴BP=BE,∠BPN=∠FEB,
在△BNP和△BFE中
∠BNP=∠BFE
∠NPB=∠FEB
PB=EB
∴△BNP≌△BFE(AAS),
∴BN=BF,
又∵BN⊥AM于N,BF⊥ME于F,
∴BM平分∠AME,
(4)AM+BM=MC

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目