题目内容
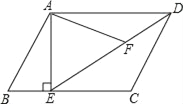
【题目】如图,在![]() 中,点
中,点![]() 为AC边中点,动点
为AC边中点,动点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 的路径以每秒1个单位长度的速度运动到
的路径以每秒1个单位长度的速度运动到![]() 点,在此过程中线段
点,在此过程中线段![]() 的长度
的长度![]() 随着运动时间
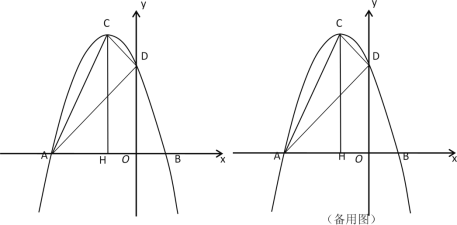
随着运动时间![]() 变化的函数关系如图2所示,则边
变化的函数关系如图2所示,则边![]() 的长为__________.
的长为__________.

【答案】![]()
【解析】
根据函数图像可以判断得出CD=2,当运动到AB边上时,当x取![]() 时,存在最小值,此时,CP⊥AB,求出AP长度,再证△ACP∽△CBP,根据相似比求出BC的值即可.
时,存在最小值,此时,CP⊥AB,求出AP长度,再证△ACP∽△CBP,根据相似比求出BC的值即可.
解:由函数图像可知,
最开始PC长度为2,即CD=2,
∵D为AC中点,
∴DA=CD=2,AC=2CD=4,
当运动到AB边上时,当x取![]() 时,存在最小值,
时,存在最小值,
此时,CP⊥AB,如图所示:
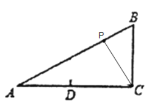
∴DA+AP=![]() ,
,
∴AP=![]() ,
,
∵CP⊥AB,
∴∠APC=90°,
在Rt△ACP中,
CP=![]() ,
,
∵∠ACB=∠BPC=90°,
∴∠ACP+∠BCP=90°,∠BCP+∠CBP=90°,
∴∠CBP=∠ACP,
∴△ACP∽△CBP,
∴![]() 即
即![]() ,
,
∴![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目