题目内容
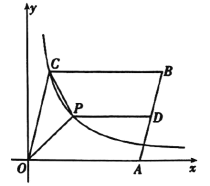
【题目】在平面直角坐标系中,点A在x轴正半轴上,点B在y轴正半轴上,O为坐标原点,OA=OB=1,过点O作OM1⊥AB于点M1;过点M1作M1A1⊥OA于点A1:过点A1作A1M2⊥AB于点M2;过点M2作M2A2⊥OA于点A2…以此类推,点M2019的坐标为_____.

【答案】(1﹣![]() ,
,![]() )
)
【解析】
根据等腰直角三角形的性质得到点M1是AB的中点,A1是OA的中点,根据中位线的性质定理,求出点M1的坐标,总结规律,根据规律解答即可.
∵在RtOAB中,OA=OB,OM1⊥AB,
∴点M1是AB的中点,OM1=A M1,
∵M1A1⊥OA,
∴A1是OA的中点,A 1M1= A 1 A,
即A 1M1是RtOAB的中位线,
∴点M1的坐标为(![]() ,
,![]() ),
),
同理,点M2的坐标为(1﹣![]() ,
,![]() ),点M3的坐标为(1﹣
),点M3的坐标为(1﹣![]() ,
,![]() ),
),
……,
点M2019的坐标为(1﹣![]() ,
,![]() ),
),
故答案为:(1﹣![]() ,
,![]() ).
).

练习册系列答案
相关题目