题目内容
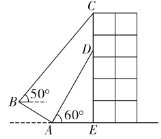
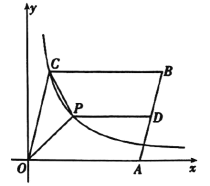
【题目】已知：如图，∠EOF=60°，在射线OE上取一点A，使OA=10cm，在射线OF上取一点B，使OB=16cm．以OA、OB为邻边作平行四边形OACB．若点P在射线OF上，点Q在线段CA上，且CQ：OP=1：2．设CQ=a（a＞0）．
（1）连接PQ，当a=2时，求线段PQ的长度．
（2）若以点P、B、C、Q四点为顶点的四边形是平行四边形时，求a的值．
（3）连接PQ，以PQ所在的直线为对称轴，作点C关于直线PQ的对称点C'，当点C′恰好落在平行四边形OACB的边上或者边所在的直线上时，直接写出a的值．
【答案】（1）
；（2）
或16；（3）7或14-2
或12．
【解析】
（1）如图1，作辅助线，构建直角三角形，计算PM和MQ的长，利用勾股定理可得PQ的长；
（2）分两种情况：
①当P在边OB上时，如图2，四边形PBCQ是平行四边形，
②当P在OB的延长线上时，如图3，四边形BPCQ是平行四边形，
分别根据PB=CQ列方程可得结论；
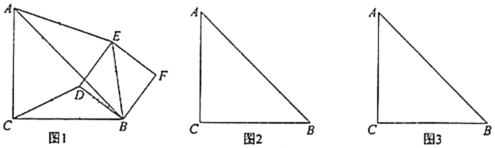
（3）存在三种情况：①如图4，当C'在边AC上时，PQ⊥AC，过B作BD⊥AC于D时，则BD∥PQ，
②如图5，当C'在边OB上时，连接PC、CC'、C'Q，过C作CR⊥OP于R，
③如图6，当C'在直线CB上时，连接PC、CC'、C'Q，
分别根据对称性和直角三角形的性质列方程可得结论．
解：（1）如图1，过A作AN⊥OB于N，过B作BD⊥AC于D，过Q作QM⊥OF于M，则AN∥BD∥MQ，
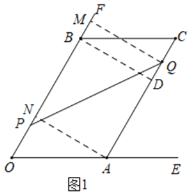
Rt△AON中，∠AOB=∠EOF=60°，OA=10，
∴ON=
OA=5，AN=5
，
同理得：CD=5，BD=5，
∵四边形OACB是平行四边形，
∴OB∥AC，
∴MQ=BD=5，
当a=2时，CQ=2，OP=4，
∴BM=DQ=5-2=3，
∴PM=PB+BM=16-4+3=15，
Rt△PMQ中，由勾股定理得：PQ=
=
=10（cm）；
（2）分两种情况：
①当P在边OB上时，如图2，四边形PBCQ是平行四边形，
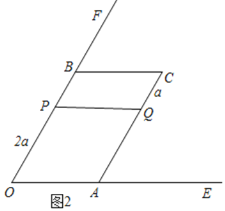
∴PB=CQ，
即16-2a=a，
a=；
②当P在OB的延长线上时，如图3，四边形BPCQ是平行四边形，
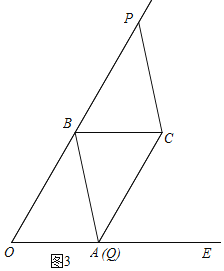
∴PB=CQ
即2a-16=a，
a=16，此时Q与A重合，
综上，a的值为或16；
（3）分三种情况：
①如图4，当C'在边AC上时，PQ⊥AC，过B作BD⊥AC于D时，则BD∥PQ，
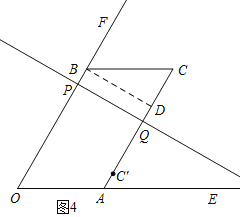
∴PB=QD，
16-2a=a-5，
3a=21，
a=7；
②如图5，当C'在边OB上时，连接PC、CC'、C'Q，过C作CR⊥OP于R，
∵C与C'关于PQ对称，
∴PQ是CC'的垂直平分线，
∴PC=PC'，CQ=C'Q，
∴∠PCC'=∠PC'C，
∵AC∥OP，
∴∠PC'C=∠QCC'，
∴∠QCC'=∠PCC'，
∵CC'⊥PQ，
∴PC=CQ=a，
∵OP=2a，
∴BP=2a-16，
Rt△BCR中，∠CBR=60°，
∴∠BCR=30°，
∵BC=10，
∴BR=5，CR=5，
∴PR=5-（2a-16）=21-2a，
由勾股定理得：
，
a=14+2（舍）或14-2；
③如图6，当C'在直线CB上时，连接PC、PC'、C'Q，
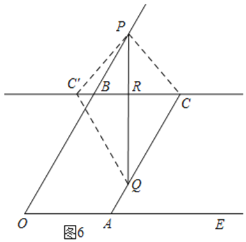
Rt△PBR中，∠PBR=60°，
∴∠BPR=30°，
∵PB=2a-16，
∴BR=BP=a-8，
同理得：CR=CQ=a，
∵BC=BR+CR，
∴a-8+a=10，a=12，
综上，a的值为7或14-2或12．
