题目内容
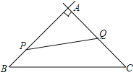
【题目】如图,AD是△ABC的中线,AB=AC,∠BAC=45°,过点C作CE⊥AB于点E,交AD于点F.试判断AF与CD之间的关系,并证明.

【答案】AF=2CD.理由见解析
【解析】
由全等三角形的性质得出AF=BC,即可得出结论.
AF⊥DC且AF=2CD,
∵CE⊥AB,
∴∠BEC=∠AEC=90°,
∴∠ECB+∠B=90°,
又∵∠BAC=45°,
∴∠ACE=45°,
∴∠BAC=∠ACE,
∴AE=EC,
∵AB=AC,AD是△ABC的中线,
∴BC=2DC,AD⊥BC,
即有:AF⊥CD,
∴∠ADC=∠ADB=90°,
∴∠BAD+∠B=90°,
∴∠BAD=∠BCE,
在△AEF和△CEB中, ,
,
∴△AEF≌△CEB,
∴AF=BC,
∴AF=2CD.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
【题目】某同学在用描点法画二次函数![]() 的图象时,列出下面的表格:
的图象时,列出下面的表格:
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
根据表格提供的信息,下列说法错误的是( )
A. 该抛物线的对称轴是直线![]() B. 该抛物线与
B. 该抛物线与![]() 轴的交点坐标为
轴的交点坐标为
C. ![]() D. 若点
D. 若点![]() 是该抛物线上一点.则
是该抛物线上一点.则![]()