题目内容
【题目】(本小题满分10分)已知关于x的方程mx2-(3m-1)x+2m-2=0
(1)求证:无论m取任何实数时,方程恒有实数根.
(2)若关于x的二次函数y= mx2-(3m-1)x+2m-2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
(3)在直角坐标系xoy中,画出(2)中的函数图象,结合图象回答问题:当直线y=x+b与(2)中的函数图象只有两个交点时,求b的取值范围.
【答案】
(1)略
(2)y1= x(x-2)或y2=![]() (x-2)(x-4)
(x-2)(x-4)
(3)当b<-或b>-或b=-2时,直线y=x+b与(2)中的图象只有两个交点
【解析】解:(1)分两种情况讨论:
①当m=0时,方程为x-2=0,∴x=2 方程有实数根
②当m≠0时,则一元二次方程的根的判别式
△=[-(3m-1)]2-4m(2m-2)=m2+2m+1=(m+1)2≥0
不论m为何实数,△≥0成立,∴方程恒有实数根
综合①②,可知m取任何实数,方程mx2-(3m-1)x+2m-2=0恒有实数根.
(2)设x1,x2为抛物线y= mx2-(3m-1)x+2m-2与x轴交点的横坐标.
则有x1+x2=![]() ,x1·x2=
,x1·x2=![]()
由| x1-x2|=![]() =
=![]() =
=![]() =
=![]() ,
,
由| x1-x2|=2得![]() =2,∴
=2,∴![]() =2或
=2或![]() =-2
=-2
∴m=1或m=![]()
∴所求抛物线的解析式为:y1=x2-2x或y2=![]() x2+2x-
x2+2x-
即y1= x(x-2)或y2=![]() (x-2)(x-4)其图象如图所示.
(x-2)(x-4)其图象如图所示.
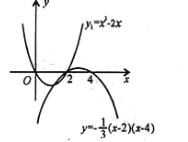
(3)在(2)的条件下,直线y=x+b与抛物线y1,y2组成的图象只有两个交点,结合图象,求b的取值范围.
 ,当y1=y时,得x2-3x-b=0,△=9+4b=0,解得b=-;
,当y1=y时,得x2-3x-b=0,△=9+4b=0,解得b=-;
同理 ,可得△=9-4(8+3b)=0,得b=-.
,可得△=9-4(8+3b)=0,得b=-.
观察函数图象可知当b<-或b>-时,直线y=x+b与(2)中的图象只有两个交点.
由![]()
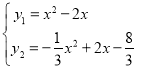
当y1=y2时,有x=2或x=1
当x=1时,y=-1
所以过两抛物线交点(1,-1),(2,0)的直线y=x-2,
综上:当b<-或b>-或b=-2时,直线y=x+b与(2)中的图象只有两个交点.

 阅读快车系列答案
阅读快车系列答案【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共![]() 只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数 |
|
|
|
|
|
|
摸到白球的次数 |
|
|
|
|
|
|
摸到白球的频率 |
|
|
|
|
|
|
![]() 上表中的
上表中的![]() ________;
________;![]() ________
________
![]() “摸到白球”的概率的估计值是________(精确到
“摸到白球”的概率的估计值是________(精确到![]() );
);
![]() 试估算口袋中黑、白两种颜色的球各有多少只?
试估算口袋中黑、白两种颜色的球各有多少只?





