题目内容
【题目】在![]() 中,已知三角形的三边长,求这个三角形的面积.
中,已知三角形的三边长,求这个三角形的面积.
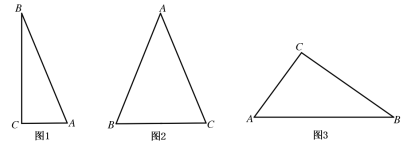
(1)如图1,已知![]() ,
,![]() ,
,![]() ,则
,则![]() 的面积是______;
的面积是______;
(2)如图2,已知![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
(3)如图3,已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)30;(2)60;(3)![]()
【解析】
(1)先根据勾股定理判断△ABC是直角三角形,然后根究三角形的面积公式求解即可;
(2)作AD⊥BC,根据三线合一求出BD的长,再利用勾股定理求出AD的长,然后根究三角形的面积公式求解即可;
(3)作CD⊥AB,设AD=x,则BD=12-x,根据勾股定理求出CD的长,然后根究三角形的面积公式求解即可.
解:(1)∵52+122=132,即AC2+BC2=AB2,
∴△ABC是直角三角形,∠C=90°,
∴![]() 的面积=
的面积=![]() ;
;
(2)如图2,作AD⊥BC,

∵AB=AC, ![]() ,
,
∴BD=![]() ,
,
∴AD=![]() ,
,
∴![]() 的面积=
的面积=![]() ;
;
(3)如图3,作CD⊥AB,设AD=x,则BD=12-x,

∵AC2-AD2=BC2+BD2,
∴82-x2=102-(12-x)2,
解之得
x=![]() ,
,
∴CD= =
=![]() ,
,
∴![]() 的面积=
的面积=![]() .
.

练习册系列答案
相关题目
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共![]() 只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数 |
|
|
|
|
|
|
摸到白球的次数 |
|
|
|
|
|
|
摸到白球的频率 |
|
|
|
|
|
|
![]() 上表中的
上表中的![]() ________;
________;![]() ________
________
![]() “摸到白球”的概率的估计值是________(精确到
“摸到白球”的概率的估计值是________(精确到![]() );
);
![]() 试估算口袋中黑、白两种颜色的球各有多少只?
试估算口袋中黑、白两种颜色的球各有多少只?