题目内容
【题目】已知：实数x满足2a﹣3≤x≤2a+2，y1＝x+a，y2＝﹣2x+a+3，对于每一个x，p都取y1，y2中的较大值．若p的最小值是a2﹣1，则a的值是（ ）
A.0或﹣3B.2或﹣1C.1或2D.2或﹣3
【答案】D
【解析】
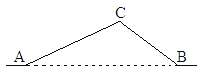
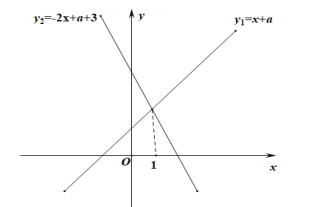
先求出两直线的交点坐标（1，a+1），画出草图，分左、中、右三种情况讨论交点的横坐标1和2a﹣3≤x≤2a+2的关系，结合图象和x的取值范围，找到并求出相应的p的最小值，根据题意列出关于a的方程并解出即可.
解：解方程x+a＝﹣2x+a+3，解得x＝1，当x＝1时，y1＝a+1，
所以直线y1＝x+a，y2＝﹣2x+a+3的交点坐标为（1，a+1），
① 当
，即
时，
由图可知：当
时，p取最小值是a+1．
所以a2﹣1=a+1
所以（a﹣2）（a+1）＝0．
所以a＝2或a=﹣1，
又∵
∴a＝2；
② 当
，即
时，
由图可知：当
时，p取最小值是y1＝2a-3+a．
∴a2﹣1=3a-3
∴a=2或a=1，
又∵，
∴a无解；
③当2a+2<1，即
,
由图可知：当
时，p取最小值是y2=-2(2a+2)+a+3
∴a2﹣1=-3a-1,
∴a=-3或a=0，
又∵，
∴a=-3；
综述所述：2或﹣3
故选：D．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
