题目内容
如图,在平面直角坐标系xOy中,函数y= (x>0)的图像与一次函数y=kx-k的图像的交点为A(m,3).
(x>0)的图像与一次函数y=kx-k的图像的交点为A(m,3).

(1)求一次函数的解析式;
(2)设一次函数y=kx-k的图像与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是9,直接写出P点的坐标.
 (x>0)的图像与一次函数y=kx-k的图像的交点为A(m,3).
(x>0)的图像与一次函数y=kx-k的图像的交点为A(m,3).
(1)求一次函数的解析式;
(2)设一次函数y=kx-k的图像与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是9,直接写出P点的坐标.
(1)y= x-
x- ;(2)(5,0)或(-3,0)
;(2)(5,0)或(-3,0)
 x-
x- ;(2)(5,0)或(-3,0)
;(2)(5,0)或(-3,0)试题分析:(1)将A点坐标代入y=
 (x>0),求出m的值为3,再将(3,3)代入y=kx-k,求出k的值,即可得到一次函数的解析式;
(x>0),求出m的值为3,再将(3,3)代入y=kx-k,求出k的值,即可得到一次函数的解析式;(2)将三角形以x轴为分界线,分为两个三角形计算,再把它们相加.
(1)将A(m,2)代入y=
 (x>0)得m=3,
(x>0)得m=3,则A点坐标为A(3,3),
将A(3,3)代入y=kx-k得,3k-k=3,解得k=
 ,
,则一次函数解析式为y=
 x-
x- ;
;(2)∵一次函数y=
 x-
x- 与x轴的交点为C(1,0),与y轴的交点为(0,-
与x轴的交点为C(1,0),与y轴的交点为(0,- ),
),∴
 ,解得
,解得
∴P点的坐标为(5,0)或(-3,0).
点评:根据待定系数法求出函数解析式并熟悉点的坐标与图形的关系是解题的关键.

练习册系列答案
相关题目
 .与
.与 在一次函数y=-2x+b的图象上,则
在一次函数y=-2x+b的图象上,则 (填>、<或=).
(填>、<或=). 的图象。
的图象。
 的图象;
的图象; ,分别过A、B两点作直线l3的垂线,垂足为E、F.直接写出线段AE、BF、EF三者之间的关系 .
,分别过A、B两点作直线l3的垂线,垂足为E、F.直接写出线段AE、BF、EF三者之间的关系 . 与挖掘时间
与挖掘时间 之间的关系如图所示,请根据图象所提供的信息解答下列问题:
之间的关系如图所示,请根据图象所提供的信息解答下列问题: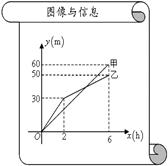
 的时段内,
的时段内, 与
与 之间的函数关系式;
之间的函数关系式; 的时段内,
的时段内, 和
和 (
( ),构成函数
),构成函数 和
和 ,并使这两个函数图象的交点在直线
,并使这两个函数图象的交点在直线 的右侧,则这样的有序数对(
的右侧,则这样的有序数对(
 ,则
,则 .
.