题目内容
【题目】综合与实践:
阅读理解:数学兴趣小组在探究如何求![]() 的值,经过思考、讨论、交流,得到以下思路:
的值,经过思考、讨论、交流,得到以下思路:
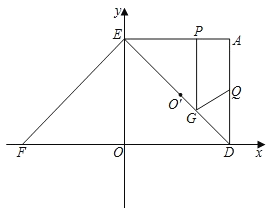
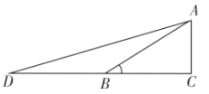
如图1,作![]() ,使
,使![]() ,
,![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.![]()
![]() .
.
请解决下列问题:
(1)类比求解:求出![]() 的值;
的值;
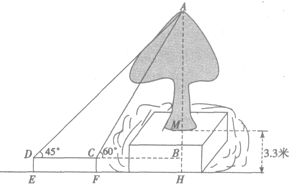
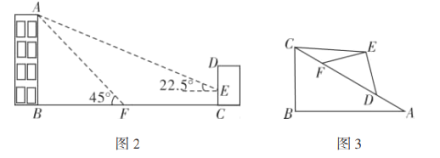
(2)问题解决:如图2,某住宅楼![]() 的后面有一建筑物
的后面有一建筑物![]() ,当光线与地面的夹角是
,当光线与地面的夹角是![]() 时,住宅在建筑物的墙上留下高
时,住宅在建筑物的墙上留下高![]() 的影子
的影子![]() ;而当光线与地面的夹角是
;而当光线与地面的夹角是![]() 时,住宅楼顶
时,住宅楼顶![]() 在地面上的影子
在地面上的影子![]() 与墙角
与墙角![]() 有
有![]() 的距离(
的距离(![]() ,
,![]() ,
,![]() 在一条直线上).求住宅楼
在一条直线上).求住宅楼![]() 的高度(结果保留根号);
的高度(结果保留根号);
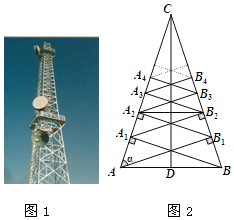
(3)探究发现:如图3,小明用硬纸片做了两个直角三角形,在![]() 中,
中,![]() ,
,![]() ,
,![]() ;在
;在![]() 中,
中,![]() ,
,![]() ,
,![]() .他将
.他将![]() 的斜边
的斜边![]() 与
与![]() 的斜边
的斜边![]() 重合在一起,并将
重合在一起,并将![]() 沿
沿![]() 方向移动.在移动过程中,
方向移动.在移动过程中,![]() ,
,![]() 两点始终在
两点始终在![]() 边上(移动开始时点
边上(移动开始时点![]() 与点
与点![]() 重合).探究在
重合).探究在![]() 移动过程中,是否存在某个位置,使得
移动过程中,是否存在某个位置,使得![]() ?如果存在,直接写出
?如果存在,直接写出![]() 的长度;如果不存在,请说明理由.
的长度;如果不存在,请说明理由.
【答案】(1)![]() ;(2)住宅楼的高为
;(2)住宅楼的高为![]() .(3)存在某个位置,使得
.(3)存在某个位置,使得![]() ,
,![]() 的长为
的长为![]() .
.
【解析】
(1)如图1,只需借鉴思路一或思路二的方法,即可解决问题;
(2)在![]() 中,设
中,设![]() 为
为![]() 得出
得出![]() ,在
,在![]() 中,根据
中,根据![]() 列出关于x的方程
列出关于x的方程![]() 求解即可;
求解即可;
(3)因为在![]() 中,
中,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ;假设在
;假设在![]() 移动过程中,存在某个位置使得
移动过程中,存在某个位置使得![]() ,因为
,因为![]() ,所以CF=FE=
,所以CF=FE=![]() ,所以
,所以![]() 的长为
的长为![]() .
.
(1)如图,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() .
.
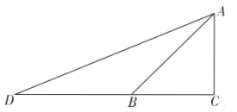
在![]() 中,
中,![]() ,
,![]() ,设
,设![]() ,则
,则![]() .
.
∴![]() ,
,
∴![]()
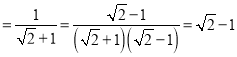 .
.
(2)如图,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
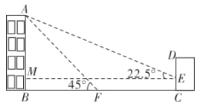
在![]() 中,
中,![]() ,设
,设![]() 为
为![]() .
.
∴![]() .
.
∴![]() .
.
∵在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴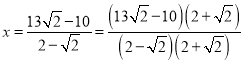
![]() .
.
答:住宅楼的高为![]() .
.
(3)存在某个位置,使得![]() ,理由如下:
,理由如下:
当![]() 时,∵
时,∵![]() ,
,
∴∠ECF=∠CEF,
∴CF=EF,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() .
.

练习册系列答案
相关题目