Question

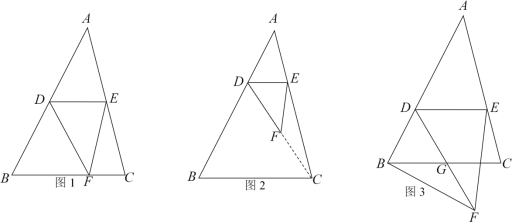
【题目】如图，在△ABC中，点D、E在BC边上，点F在AC边上，将△ABD沿着AD翻折，使点B和点E重合，将△CEF沿着EF翻折，点C恰与点A重合．结论：①∠BAC=90°，②DE=EF，③∠B=2∠C，④AB=EC，正确的有（　　）

A.①②③④B.③④C.①②④D.①②③

Answer 1

【答案】B

【解析】

将△ABD沿着AD翻折，则△ABD≌△AED，可得AB=AE，∠B=∠AEB，将△CEF沿着EF翻折，则△AEF≌△CEF，可得AE=CE，∠C=∠CAE，进而得到AB=EC,∠AEB=∠C+∠CAE=2∠C，从而判断③④正确,由折叠性质只能得到∠ADB=∠ADC=∠AFE=∠CFE=90°,BD=DE,无法得到∠BAC=90°，DE=EF，从而判断①②不一定正确.

解：∵将△ABD沿着AD翻折，使点B和点E重合，

∴AB=AE，∠B=∠AEB，

∵将△CEF沿着EF翻折，点C恰与点A重合，

∴AE=CE，∠C=∠CAE，

∴AB=EC，∴④正确；

∵∠AEB=∠C+∠CAE=2∠C，

∴∠B=2∠C，故③正确；

由折叠性质可得△ABD≌△AED，△AEF≌△CEF，

∴∠ADB=∠ADC=∠AFE=∠CFE=90°,BD=DE,

无法得到∠BAC=90°，DE=EF，

∴①②不一定正确.

故选：B．