��Ŀ����
����Ŀ����ͼ����֪������y= ![]() ��x+2����x��4����kΪ��������k��0����x������������ν���A��B���㣬��y�ύ�ڵ�C��������B��ֱ��y=��
��x+2����x��4����kΪ��������k��0����x������������ν���A��B���㣬��y�ύ�ڵ�C��������B��ֱ��y=�� ![]() x+b�������ߵ���һ����ΪD��
x+b�������ߵ���һ����ΪD��
��1������D�ĺ�����Ϊ��5���������ߵĺ�������ʽ��
��2�����ڵ�һ�����ڵ����������е�P��ʹ����A��B��PΪ��������������ABC���ƣ���k��ֵ��
��3���ڣ�1���������£���FΪ�߶�BD��һ�㣨�����˵㣩������AF��һ����M�ӵ�A���������߶�AF��ÿ��1����λ���ٶ��˶���F�������߶�FD��ÿ��2����λ���ٶ��˶���D��ֹͣ������F�������Ƕ���ʱ����M�������˶���������ʱ���٣�
���𰸡�
��1��
�⣺������y= ![]() ��x+2����x��4����
��x+2����x��4����
��y=0�����x=��2��x=4��
��A����2��0����B��4��0����
��ֱ��y=�� ![]() x+b������B��4��0����
x+b������B��4��0����
�ੁ ![]() ��4+b=0�����b=
��4+b=0�����b= ![]() ��
��
��ֱ��BD����ʽΪ��y=�� ![]() x+
x+ ![]() ��
��
��x=��5ʱ��y=3 ![]() ��
��
��D����5��3 ![]() ����
����
�ߵ�D����5��3 ![]() ����������y=
����������y= ![]() ��x+2����x��4���ϣ�
��x+2����x��4���ϣ�
�� ![]() ����5+2������5��4��=3
����5+2������5��4��=3 ![]() ��
��
��k= ![]() ��
��
�������ߵĺ�������ʽΪ��y= ![]() ��x+2����x��4��
��x+2����x��4��
��2��
�⣺�������߽���ʽ����x=0����y=��k��
��C��0����k����OC=k��
��Ϊ��P�ڵ�һ�����ڵ��������ϣ����ԡ�ABPΪ�۽ǣ�
������������������ƣ�ֻ�����ǡ�ABC�ס�APB���ABC�ס�PAB��
������ABC�ס�APB�����С�BAC=��PAB�����ͼ2��1��ʾ��
��P��x��y��������P��PN��x���ڵ�N����ON=x��PN=y��
tan��BAC=tan��PAB������ ![]() ��
��
��y= ![]() x+k��
x+k��
��P��x�� ![]() x+k�������������߽���ʽy=
x+k�������������߽���ʽy= ![]() ��x+2����x��4����
��x+2����x��4����
�� ![]() ��x+2����x��4��=
��x+2����x��4��= ![]() x+k�������ã�x2��6x��16=0��
x+k�������ã�x2��6x��16=0��
��ã�x=8��x=��2�����A�غϣ���ȥ����
��P��8��5k����
�ߡ�ABC�ס�APB��
�� ![]() ����
���� ![]() ��
��
��ã�k= ![]() ��
��
������ABC�ס�PAB�����С�ABC=��PAB�����ͼ2��2��ʾ��
��P��x��y��������P��PN��x���ڵ�N����ON=x��PN=y��
tan��ABC=tan��PAB������ ![]() =
= ![]() ��
�� 
��y= ![]() x+
x+ ![]() ��
��
��P��x�� ![]() x+
x+ ![]() �������������߽���ʽy=
�������������߽���ʽy= ![]() ��x+2����x��4����
��x+2����x��4����
�� ![]() ��x+2����x��4��=
��x+2����x��4��= ![]() x+
x+ ![]() �������ã�x2��4x��12=0��
�������ã�x2��4x��12=0��
��ã�x=6��x=��2�����A�غϣ���ȥ����
��P��6��2k����
�ߡ�ABC�ס�PAB��
![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
���k=�� ![]() ��
��
��k��0��
��k= ![]() ��
��
����������k= ![]() ��k=
��k= ![]()
��3��
�⣺����һ��
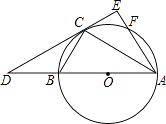
���ͼ3���ɣ�1��֪��D����5��3 ![]() ����
����
���ͼ2��2������D��DN��x���ڵ�N����DN=3 ![]() ��ON=5��BN=4+5=9��
��ON=5��BN=4+5=9��
��tan��DBA= ![]() =
= ![]() =
= ![]() ��
��
���DBA=30�㣮

����D��DK��x�ᣬ���KDF=��DBA=30�㣮
����F��FG��DK�ڵ�G����FG= ![]() DF��
DF��
�����⣬����M�˶���·��Ϊ����AF+DF���˶�ʱ�䣺t=AF+ ![]() DF��
DF��
��t=AF+FG�����˶���ʱ��ֵ��������AF+FG�ij���ֵ��
�ɴ��߶���̿�֪������AF+FG�ij��ȵ���СֵΪDK��x��֮��Ĵ��߶Σ�
����A��AH��DK�ڵ�H����t��С=AH��AH��ֱ��BD�Ľ��㣬��Ϊ����֮F�㣮
��A�������Ϊ��2��ֱ��BD����ʽΪ��y=�� ![]() x+
x+ ![]() ��
��
��y=�� ![]() ������2��+
������2��+ ![]() =2
=2 ![]() ��
��
��F����2��2 ![]() ����
����
��������������F����Ϊ����2��2 ![]() ��ʱ����M�������˶���������ʱ���٣�
��ʱ����M�������˶���������ʱ���٣�
��������
��DK��AB��AH��DK��AH��ֱ��BD�ڵ�F��
�ߡ�DBA=30�㣬
���BDH=30�㣬
��FH=DF��sin30��= ![]() ��
��
�൱�ҽ���AH��DKʱ��AF+FH��С��
��M�������˶�����ʱΪ��t= ![]() ��
��
��lBD��y=�� ![]() x+
x+ ![]() ��
��
��FX=AX=��2��
��F����2�� ![]() ��
��
����������1�����������A��B���꣬Ȼ�����ֱ��BD�Ľ���ʽ����õ�D���꣬���������߽���ʽ�����k��ֵ����2����Ϊ��P�ڵ�һ�����ڵ��������ϣ����ԡ�ABPΪ�۽ǣ�������������������ƣ�ֻ�����ǡ�ABC�ס�APB���ABC�ס�PAB�����ͼ2��������������������з������ۣ��ֱ���㣻��3�������⣬����M�˶���·��Ϊ����AF+DF���˶�ʱ�䣺t=AF+ ![]() DF�����ͼ3���������ߣ���AF+
DF�����ͼ3���������ߣ���AF+ ![]() DFת��ΪAF+FG�����ɴ��߶���̣��õ����߶�AH��ֱ��BD�Ľ��㣬��Ϊ�����F�㣮
DFת��ΪAF+FG�����ɴ��߶���̣��õ����߶�AH��ֱ��BD�Ľ��㣬��Ϊ�����F�㣮
�����㾫����������Ҫ�����˶��κ��������ʵ����֪ʶ�㣬��Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮