题目内容
【题目】如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足 ![]() ,过点C作⊙O的切线交AB的延长线于D点,交AF的延长线于E点.
,过点C作⊙O的切线交AB的延长线于D点,交AF的延长线于E点. 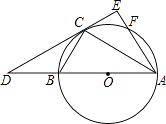
(1)求证:AE⊥DE;
(2)若tan∠CBA= ![]() ,AE=3,求AF的长.
,AE=3,求AF的长.
【答案】
(1)证明:连接OC,
∵OC=OA,
∴∠BAC=∠OCA,
∵ ![]() ,
,
∴∠BAC=∠EAC,
∴∠EAC=∠OCA,
∴OC∥AE,
∵DE切⊙O于点C,
∴OC⊥DE,
∴AE⊥DE
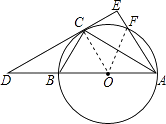
(2)解:∵AB是⊙O的直径,
∴△ABC是直角三角形,
∵tan∠CBA= ![]() ,
,
∴∠CBA=60°,
∴∠BAC=∠EAC=30°,
∵△AEC为直角三角形,AE=3,
∴AC=2 ![]() ,
,
连接OF,
∵OF=OA,∠OAF=∠BAC+∠EAC=60°,
∴△OAF为等边三角形,
∴AF=OA= ![]() AB,
AB,
在Rt△ACB中,AC=2 ![]() ,tan∠CBA=
,tan∠CBA= ![]() ,
,
∴BC=2,
∴AB=4,
∴AF=2
【解析】(1)首先连接OC,由OC=OA, ![]() ,易证得OC∥AE,又由DE切⊙O于点C,易证得AE⊥DE;(2)由AB是⊙O的直径,可得△ABC是直角三角形,易得△AEC为直角三角形,根据AE=3求得AC的长,然后连接OF,可得△OAF为等边三角形,知AF=OA=
,易证得OC∥AE,又由DE切⊙O于点C,易证得AE⊥DE;(2)由AB是⊙O的直径,可得△ABC是直角三角形,易得△AEC为直角三角形,根据AE=3求得AC的长,然后连接OF,可得△OAF为等边三角形,知AF=OA= ![]() ,在△ACB中,利用已知条件求得答案.
,在△ACB中,利用已知条件求得答案.
【考点精析】认真审题,首先需要了解切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径).

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
【题目】四川省“单独两孩”政策于2014年3月20日正式开始实施,该政策的实施可能给我们的生活带来一些变化,绵阳市人口计生部门抽样调查了部分市民(每个参与调查的市民必须且只能在以下6种变化中选择一项),并将调查结果绘制成如下统计图:
种类 | A | B | C | D | E | F |
变化 | 有利于延缓社会老龄化现象 | 导致人口暴增 | 提升家庭抗风险能力 | 增大社会基本公共服务的压力 | 缓解男女比例不平衡现象 | 促进人口与社会、资源、环境的协调可持续发展 |

根据统计图,回答下列问题:
(1)参与调查的市民一共有人;
(2)参与调查的市民中选择C的人数是人;
(3)∠α=;
(4)请补全条形统计图.