题目内容
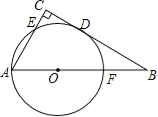
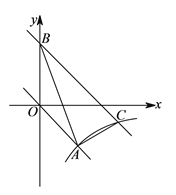
【题目】如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC,AB于点E,F.
(1)若∠B=30°,求证:以A,O,D,E为顶点的四边形是菱形;
(2)填空:若AC=6,AB=10,连接AD,则⊙O的半径为 ,AD的长为 .

【答案】(1) 见解析;(2)![]()
【解析】
(1) 先通过证明△AOE为等边三角形, 得出AE=OD, 再根据“同位角相等, 两直线平行” 证明AE//OD, 从而证得四边形AODE是平行四边形, 再根据 “一组邻边相等的平行四边形为菱形” 即可得证.
(2) 利用在Rt△OBD中,sin∠B=![]() =
=![]() 可得出半径长度,在Rt△ODB中BD=
可得出半径长度,在Rt△ODB中BD=![]() ,可求得BD的长,由CD=CB﹣BD可得CD的长,在RT△ACD中,AD=
,可求得BD的长,由CD=CB﹣BD可得CD的长,在RT△ACD中,AD=![]() ,即可求出AD长度.
,即可求出AD长度.
解:(1)证明: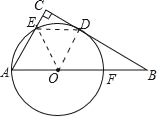
连接OE、ED、OD,
在Rt△ABC中,∵∠B=30°,
∴∠A=60°,
∵OA=OE,∴△AEO是等边三角形,
∴AE=OE=AO
∵OD=OA,
∴AE=OD
∵BC是圆O的切线,OD是半径,
∴∠ODB=90°,又∵∠C=90°
∴AC∥OD,又∵AE=OD
∴四边形AODE是平行四边形,
∵OD=OA
∴四边形AODE是菱形.
(2)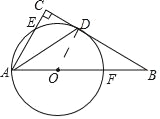
在Rt△ABC中,∵AC=6,AB=10,
∴sin∠B=![]() =
=![]() ,BC=8
,BC=8
∵BC是圆O的切线,OD是半径,
∴∠ODB=90°,
在Rt△OBD中,sin∠B=![]() =
=![]() ,
,
∴OB=![]() OD
OD
∵AO+OB=AB=10,
∴OD+![]() OD=10
OD=10
∴OD=![]()
∴OB=![]() OD=
OD=![]()
∴BD=![]()
=5
∴CD=CB﹣BD=3
∴AD=![]()
=![]()
=3![]() .
.

【题目】小明平时喜欢玩“开心消消乐”游戏,本学期在学校组织的几次数学反馈性测试中,小明的数学成绩如下表:
月份 |
|
|
|
|
|
|
成绩(分) |
|
|
|
| ··· | ··· |
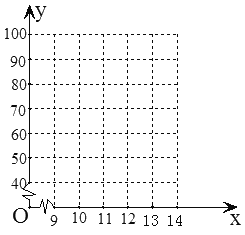
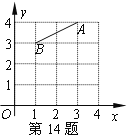
(1)以月份为x轴,成绩为y轴,根据上表提供的数据在平面直角坐标系中描点;
(2)观察(1)中所描点的位置关系,猜想![]() 与
与![]() 之间的的函数关系,并求出所猜想的函数表达式;
之间的的函数关系,并求出所猜想的函数表达式;
(3)若小明继续沉溺于“开心消消乐“游戏,照这样的发展趋势,请你估计元月(此时![]() )份的考试中小明的数学成绩,并用一句话对小明提出一些建议.
)份的考试中小明的数学成绩,并用一句话对小明提出一些建议.