题目内容
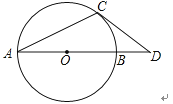
【题目】如图,在△ABC中,∠CAB=90°,∠CBA=50°,以AB为直径作⊙O交BC于点D,点E在边AC上,且满足ED=EA.
(1)求∠DOA的度数。
(2)求证:直线ED与⊙O相切.
【答案】
(1)
解;∵∠DBA=50°,
∴∠DOA=2∠DBA=100°
(2)
证明:连接OE.

在△EAO与△EDO中,
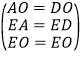 ,
,
∴△EAO≌△EDO,
∴∠EDO=∠EAO,
∵∠BAC=90°,
∴∠EDO=90°,
∴DE与⊙O相切.
【解析】(1)根据圆周角定理即可得到结论;
(2)连接OE,通过△EAO≌△EDO,即可得到∠EDO=90°,于是得到结论.
【考点精析】认真审题,首先需要了解切线的判定定理(切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线).

练习册系列答案
相关题目
【题目】某商店以6元/千克的价格购进某种干果1140千克,并对其进行筛选分成甲级干果与乙级干果后同时开始销售.这批干果销售结束后,店主从销售统计中发现:甲级干果与乙级干果在销售过程中每天都有销量,且在同一天卖完;甲级干果从开始销售至销售的第x天的总销量y1(千克)与x的关系为y1=﹣x2+40x;乙级干果从开始销售至销售的第t天的总销量y2(千克)与t的关系为y2=at2+bt,且乙级干果的前三天的销售量的情况见下表:
t | 1 | 2 | 3 |
y2 | 21 | 44 | 69 |
(1)求a、b的值;
(2)若甲级干果与乙级干果分别以8元/千克和6元/千克的零售价出售,则卖完这批干果获得的毛利润是多少元?
(3)问从第几天起乙级干果每天的销量比甲级干果每天的销量至少多6千克? (说明:毛利润=销售总金额﹣进货总金额.这批干果进货至卖完的过程中的损耗忽略不计)