题目内容
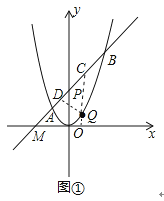
【题目】如图,在平面直角坐标系xOy中,将抛物线y=x2的对称轴绕着点P(0,2)顺时针旋转45°后与该抛物线交于A、B两点,点Q是该抛物线上一点.
(1)求直线AB的函数表达式。
(2)如图①,若点Q在直线AB的下方,求点Q到直线AB的距离的最大值
(3)如图②,若点Q在y轴左侧,且点T(0,t)(t<2)是射线PO上一点,当以P、B、Q为顶点的三角形与△PAT相似时,求所有满足条件的t的值
【答案】
(1)
解:如图①,设直线AB与x轴的交点为M.
∵∠OPA=45°,
∴OM=OP=2,即M(﹣2,0).
设直线AB的解析式为y=kx+b(k≠0),将M(﹣2,0),P(0,2)两点坐标代入,得
![]() ,解得
,解得![]() .
.
故直线AB的解析式为y=x+2
(2)
解:如图①,过点Q作x轴的垂线QC,交AB于点C,再过点Q作直线AB的垂线,垂足为D,

根据条件可知△QDC为等腰直角三角形,则QD=![]() QC.
QC.
设Q(m,m2),则C(m,m+2).
∴QC=m+2﹣m2=﹣(m﹣![]() )2+
)2+![]() ,
,
QD=![]() QC=
QC=![]() [﹣(m﹣
[﹣(m﹣![]() )2+
)2+![]() ].
].
故当m=![]() 时,点Q到直线AB的距离最大,最大值为
时,点Q到直线AB的距离最大,最大值为![]()
(3)
解:∵∠APT=45°,
∴△PBQ中必有一个内角为45°,由图知,∠BPQ=45°不合题意.
①如图②,若∠PBQ=45°,过点B作x轴的平行线,与抛物线和y轴分别交于点Q′、F.此时满足∠PBQ′=45°.
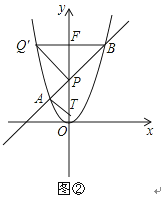
∵Q′(﹣2,4),F(0,4),
∴此时△BPQ′是等腰直角三角形,由题意知△PAT也是等腰直角三角形.
(i)当∠PTA=90°时,得到:PT=AT=1,此时t=1;
(ii)当∠PAT=90°时,得到:PT=2,此时t=0.
②如图③,
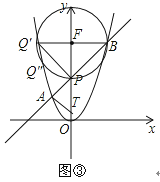
若∠PQB=45°,①中是情况之一,答案同上;
先以点F为圆心,FB为半径作圆,则P、B、Q′都在圆F上,设圆F与y轴左侧的抛物线交于另一点Q″.
则∠PQ″B=∠PQ′B=45°(同弧所对的圆周角相等),即这里的交点Q″也是符合要求.
设Q″(n,n2)(﹣2<n<0),由FQ″=2,得
n2+(4﹣n20=22,即n4﹣7n2+12=0.
解得n2=3或n2=4,而﹣2<n<0,故n=﹣![]() ,即Q″(﹣
,即Q″(﹣![]() ,3).
,3).
可证△PFQ″为等边三角形,
所以∠PFQ″=60°,又PQ″=PQ″,
所以∠PBQ″=![]() ∠PFQ″=30°.
∠PFQ″=30°.
则在△PQ″B中,∠PQ″B=45°,∠PBQ″=30°.
(i)若△Q″PB∽△PAT,则过点A作y轴的垂线,垂足为E.
则ET=![]() AE=
AE=![]() ,OE=1,
,OE=1,
所以OT=![]() ﹣1,
﹣1,
解得t=1﹣![]() ;
;
(ii)若△Q″BP∽△PAT,则过点T作直线AB垂线,垂足为G.
设TG=a,则PG=TG=a,AG=![]() TG=
TG=![]() a,AP=
a,AP=![]() ,
,
∴![]() a+a=
a+a=![]() ,
,
解得PT=![]() a=
a=![]() ﹣1,
﹣1,
∴OT=OP﹣PT=3﹣![]() ,
,
∴t=3﹣![]() .
.
综上所述,所求的t的值为t=1或t=0或t=1﹣![]() 或t=3﹣
或t=3﹣![]() .
.
【解析】(1)根据题意易得点M、P的坐标,利用待定系数法来求直线AB的解析式;
(2)如图①,过点Q作x轴的垂线QC,交AB于点C,再过点Q作直线AB的垂线,垂足为D,构建等腰直角△QDC,利用二次函数图象上点的坐标特征和二次函数最值的求法进行解答;
(3)根据相似三角形的对应角相等推知:△PBQ中必有一个内角为45°;需要分类讨论:∠PBQ=45°和∠PQB=45°;然后对这两种情况下的△PAT是否是直角三角形分别进行解答.另外,以P、B、Q为顶点的三角形与△PAT相似也有两种情况:△Q″PB∽△PAT、△Q″BP∽△PAT.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案