题目内容
【题目】如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是 
【答案】2或5
【解析】解:∵Rt△ABC纸片中,∠C=90°,AC=6,BC=8,
∴AB=10,
∵以AD为折痕△ABD折叠得到△AB′D,
∴BD=DB′,AB′=AB=10.
如图1所示:当∠B′DE=90°时,过点B′作B′F⊥AF,垂足为F.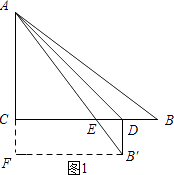
设BD=DB′=x,则AF=6+x,FB′=8﹣x.
在Rt△AFB′中,由勾股定理得:AB′2=AF2+FB′2 , 即(6+x)2+(8﹣x)2=102 .
解得:x1=2,x2=0(舍去).
∴BD=2.
如图2所示:当∠B′ED=90°时,C与点E重合.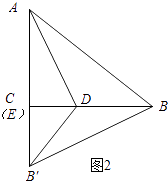
∵AB′=10,AC=6,
∴B′E=4.
设BD=DB′=x,则CD=8﹣x.
在Rt△′BDE中,DB′2=DE2+B′E2 , 即x2=(8﹣x)2+42 .
解得:x=5.
∴BD=5.
综上所述,BD的长为2或5.
所以答案是:2或5.
【考点精析】通过灵活运用翻折变换(折叠问题),掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等即可以解答此题.

练习册系列答案
相关题目







