题目内容
【题目】如图，在五边形ABCDE 中，
，
，
，点 A 到直线CD 的距离为__________
【答案】
【解析】
延长ED与BC交于点F，作AH⊥DC于点H，先证明出四边形AEFB是正方形，然后将△ABC逆时针旋转90°得到△AEG，通过证明△GAD≌△CAD证明出AH=AE最终得出答案.
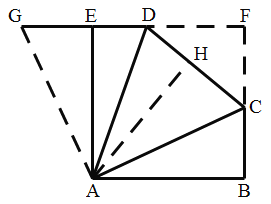
如图，延长ED与BC交于点F，作AH⊥DC于点H，
∵
，
∴四边形AEFB是矩形，
∵AB=AE，
∴四边形AEFB是正方形，
将△ABC逆时针旋转90°得到△AEG，如图所示，
则AG=AC，∠GAE=∠CAB，
∵
，
∴∠CAB+∠DAE=45°，
∴∠GAD=∠GAE+∠DAE=45°，
∴∠GAD=∠CAD，
在△GAD与△CAD中，
∵GA=CA，∠GAD=∠CAD，AD=AD，
∴△GAD≌△CAD（SAS），
∴AH=AE=
，
故答案为：.
练习册系列答案
相关题目
