题目内容
【题目】如图，E是四边形ABCD的边AB上一点．
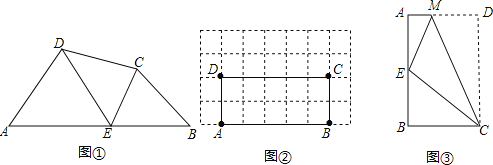
（1）猜想论证：如图，分别连接DE、CE，若∠A=∠B=∠DEC=65°，试猜想图中哪两个三角形相似，并说明理由．
（2）观察作图：如图，在矩形ABCD中，AB=5，BC=2，且A，B，C，D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图中矩形ABCD的边AB上画出所有满足条件的点E（点E与点A，B 不重合），分别连结ED，EC，使四边形ABCD被分成的三个三角形相似（不证明）．
（3）拓展探究：如图，将矩形ABCD沿CM折叠，使点D落在AB边上的点E处，若点E恰好将四边形ABCM分成的三个三角形相似，请直接写出
的值．
【答案】（1）△ADE∽△BEC；（2）见解析；（3）
=
．
【解析】
试题分析：（1）△ADE∽△BEC，理由为：利用三角形内角和定理及邻补角定义得到一对角相等，再由已知角相等，利用两角相等的三角形相似即可得证；
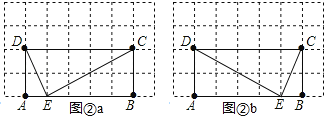
（2）如图②a与图②b所示，点E为所求的点；
（3）由点E恰好将四边形ABCM分成的三个三角形相似，利用相似三角形对应角相等得到三个角相等，再由折叠的性质得到∠DCM=∠MCE=∠BCE=30°，EC=CD=AB，在Rt△BCE中，利用锐角三角函数定义求出所求式子比值即可．
解：（1）△ADE∽△BEC，理由为：
∵∠A=65°，
∴∠ADE+∠DEA=115°，
∵∠DEC=65°，
∴∠BEC+∠DEA=115°，
∴∠ADE=∠BEC，
∵∠A=∠B，
∴△ADE∽△BEC；
（2）作图如下：
（3）∵点E恰好将四边形ABCM分成的三个三角形相似，
∴△AEM∽△BCE∽△ECM，
∴∠BCE=∠ECM=∠AEM，
由折叠可知：△ECM≌△DCM，
∴∠ECM=∠DCM，CE=CD，
∴∠BCE=∠ECM=∠DCM=30°，
∴DC=CE=AB，
在Rt△BCE中，cos∠BCE=
=cos30°，
∴=．
