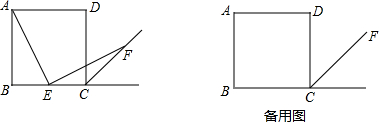Question

如图，四边形ABCD中，∠B=90°，AB=4，BC=3，CD=12，AD=13．
（1）请你说明△ACD是直角三角形；
（2）请你在规格12×12的正方形网格中（小正方形的边长为1），画出满足下列条件的四边形A′B′C′D′：
①既是轴对称又是中心对称；
②四边形A′B′C′D′的面积为四边形ABCD面积的三分之一；
③四边形A′B′C′D′的顶点在网格中的小正方形的顶点上．

Answer 1

解：（1）△ACD是直角三角形．
理由是：
∵∠B=90°，AB=3，BC=4，
∴AC²=AB²+BC²=9+16=25，∴AC=5，
又∵AC²+CD²=25+144=169，AD²=169，
∴AC²+CD²=AD²，
∴△ACD是直角三角形．

（2）∵四边形ABCD面积的为：×3×4+×5×12=36，四边形A′B′C′D′的面积为四边形ABCD面积的三分之一；
∴四边形A′B′C′D′的面积为：12，
∵四边形A′B′C′D′，既是轴对称又是中心对称，四边形A′B′C′D′的顶点在网格中的小正方形的顶点上，
∴可以画一个面积为12的矩形，如图所示：答案不唯一．
分析：（1）先根据勾股定理求出AC的长，在△ACD中，再由勾股定理的逆定理，判断三角形的形状；
（2）根据直角三角形的面积公式得出四边形ABCD面积，进而得出四边形A′B′C′D′的面积，再利用轴对称图形以及中心对称图形的性质得出符合题意的图形．
点评：本题考查了勾股定理及逆定理的综合应用以及轴对称图形和中心对称图形的性质，根据已知得出图形面积是解题关键．