题目内容
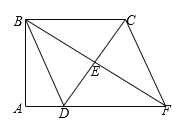
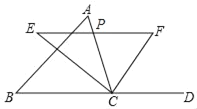
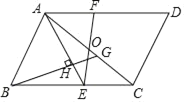
【题目】如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.
(1)若AH=3,HE=1,求△ABE的面积;
(2)若∠ACB=45°,求证:DF=![]() CG.
CG.
【答案】(1)2![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)利用勾股定理即可得出BH的长,进而运用公式得出△ABE的面积;
(2)过A作AM⊥BC于M,交BG于K,过G作GN⊥BC于N,判定△AME≌△BNG(AAS),可得ME=NG,进而得出BE=![]() GC,再判定△AFO≌△CEO(AAS),可得AF=CE,即可得到DF=BE=
GC,再判定△AFO≌△CEO(AAS),可得AF=CE,即可得到DF=BE=![]() CG.
CG.
解:(1)∵AH=3,HE=1,
∴AB=AE=4,
又∵Rt△ABH中,BH=![]() ,
,
∴S△ABE=![]() ;
;
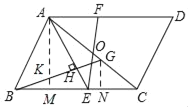
(2)如图,过A作AM⊥BC于M,交BG于K,过G作GN⊥BC于N,则∠AMB=∠AME=∠BNG=90°,
∵∠ACB=45°,
∴∠MAC=∠NGC=45°,
∵AB=AE,
∴BM=EM=![]() BE,∠BAM=∠EAM,
BE,∠BAM=∠EAM,
又∵AE⊥BG,
∴∠AHK=90°=∠BMK,而∠AKH=∠BKM,
∴∠MAE=∠NBG,
设∠BAM=∠MAE=∠NBG=α,则∠BAG=45°+α,∠BGA=∠GCN+∠GBC=45°+α,
∴AB=BG,
∴AE=BG,
在△AME和△BNG中,
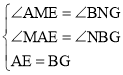 ,
,
∴△AME≌△BNG(AAS),
∴ME=NG,
在等腰Rt△CNG中,NG=NC,
∴GC=![]() NG=
NG=![]() ME=
ME=![]() BE,
BE,
∴BE=![]() GC,
GC,
∵O是AC的中点,
∴OA=OC,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠OAF=∠OCE,∠AFO=∠CEO,
∴△AFO≌△CEO(AAS),
∴AF=CE,
∴AD﹣AF=BC﹣EC,即DF=BE,
∴DF=BE=![]() CG.
CG.

 名校课堂系列答案
名校课堂系列答案【题目】为了迎接“十一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋 | 甲 | 乙 |
进价(元/双) | m | m﹣20 |
售价(元/双) | 240 | 160 |
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?