Question

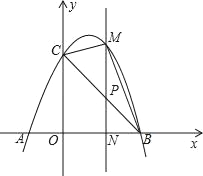
【题目】如图，已知抛物线y=﹣x2+2x+3与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，连接BC．

（1）求A，B，C三点的坐标；

（2）若点P为线段BC上一点（不与B，C重合），PM∥y轴，且PM交抛物线于点M，交x轴于点N，当△BCM的面积最大时，求△BPN的周长；

（3）在（2）的条件下，当△BCM的面积最大时，在抛物线的对称轴上存在一点Q，使得△CNQ为直角三角形，求点Q的坐标．

Answer 1

【答案】（1）A（﹣1，0），B（3，0），C（0，3）；（2）3+；（3）Q1（1， ），Q2（1， ），Q3（1，﹣），Q4（1， ）．

【解析】试题分析：（1）依据抛物线的解析式直接求得C的坐标，令y=0解方程即可求得A、B点的坐标；

（2）求出△BCM面积的表达式，这是一个二次函数，求出其取最大值的条件；然后利用勾股定理求出△BPN的周长；

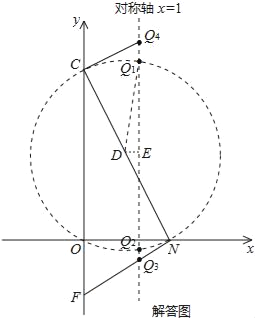
（3）如解答图，△CNQ为直角三角形，分三种情况：①点Q为直角顶点；②点N为直角顶点；③点C为直角顶点进行解答．

试题解析：（1）由抛物线的解析式y=﹣x2+2x+3，

∴C（0，3），

令y=0，﹣x2+2x+3=0，解得x=3或x=﹣1；

∴A（﹣1，0），B（3，0）．

（2）设直线BC的解析式为：y=kx+b，则有：

，解得，

∴直线BC的解析式为：y=﹣x+3．

设P（x，﹣x+3），则M（x，﹣x2+2x+3），

∴PM=（﹣x2+2x+3）﹣（﹣x+3）=﹣x2+3x．

∴S△BCM=S△PMC+S△PMB=PM（xP﹣xC）+PM（xB﹣xP）=PM（xB﹣xC）=PM．

∴S△BCM=（﹣x2+3x）=﹣（x﹣）2+．

∴当x=时，△BCM的面积最大．

此时P， ），∴PN=ON=，

∴BN=OB﹣ON=3﹣=．

在Rt△BPN中，由勾股定理得：PB=．

C△BCN=BN+PN+PB=3+．

∴当△BCM的面积最大时，△BPN的周长为3+．

（3）∵y=﹣x2+2x+3=﹣（x﹣1）2+4

∴抛物线的对称轴为直线x=1．

在Rt△CNO中，OC=3，ON=，由勾股定理得：CN=．

设点D为CN中点，则D（， ），CD=ND=．

如解答图，△CNQ为直角三角形，

①若点Q为直角顶点．

作Rt△CNO的外接圆⊙D，与对称轴交于Q1、Q2两点，由圆周角定理可知，Q1、Q2两点符合题意．

连接Q1D，则Q1D=CD=ND=．

过点D（， ）作对称轴的垂线，垂足为E，

则E（1， ），Q1E=Q2E，DE=1﹣=．

在Rt△Q1DE中，由勾股定理得：

Q1E==．

∴Q1（1， ），Q2（1， ）；

②若点N为直角顶点．

过点N作NF⊥CN，交对称轴于点Q3，交y轴于点F．

易证Rt△NFO∽Rt△CNO，则，即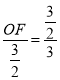，解得OF=．

∴F（0，﹣），又∵N（，0），

∴可求得直线FN的解析式为：y=x﹣．

当x=1时，y=﹣，

∴Q3（1，﹣ ）；

③当点C为直角顶点时．

过点C作Q4C⊥CN，交对称轴于点Q4．

∵Q4C∥FN，∴可设直线Q4C的解析式为：y=x+b，

∵点C（0，3）在该直线上，∴b=3．

∴直线Q4C的解析式为：y=x+3，

当x=1时，y=，

∴Q4（1， ）．

综上所述，满足条件的点Q有4个，

其坐标分别为：Q1（1， ），Q2（1， ），Q3（1，﹣），Q4（1， ）．