题目内容
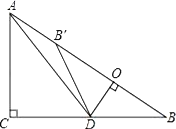
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
【答案】(1)证明见解析;(2)5;(3)![]()
【解析】试题分析:(1)公共角和直角两个角相等,所以相似.(2)由(1)可得三角形相似比,设BD=x,CD,BD,BO用x表示出来,所以可得BD长.(3)同(2)原理,BD=B′D=x,
AB′,B′O,BO用x表示,利用等腰三角形求BD长.
试题解析:
(1)证明:∵DO⊥AB,∴∠DOB=90°,
∴∠ACB=∠DOB=90°,
又∵∠B=∠B.∴△DOB∽△ACB.
(2)∵AD 平分∠CAB,DC⊥AC,DO⊥AB,
∴DO=DC,
在 Rt△ABC 中,AC=6,BC=,8,∴AB=10,
∵△DOB∽△ACB,
∴DO∶BO∶BD=AC∶BC∶AB=3∶4∶5,
设BD=x,则DO=DC=![]() x,BO=
x,BO=![]() x,
x,
∵CD+BD=8,∴ ![]() x+x=8,解得x=,5,即:BD=5.
x+x=8,解得x=,5,即:BD=5.
(3)∵点B 与点B′关于直线DO 对称,∴∠B=∠OB′D,
BO=B′O=![]() x,BD=B′D=x,
x,BD=B′D=x,
∵∠B 为锐角,∴∠OB′D 也为锐角,∴∠AB′D 为钝角,
∴当△AB′D 是等腰三角形时,AB′=DB′,
∵AB′+B′O+BO=10,
∴x+![]() x+
x+![]() x=10,解得x=
x=10,解得x=![]() ,即BD=
,即BD=![]() ,
,
∴当△AB′D 为等腰三角形时,BD=![]() .
.

练习册系列答案
相关题目