题目内容
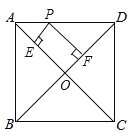
【题目】已知点A(3,4),点B为直线x=1上的动点,设B(-1,y).

(1)如图①,若△ABO是等腰三角形且AO=AB时,求点B的坐标;
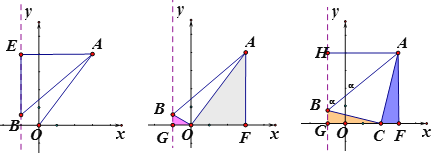
(2)如图②,若点C(x,0)且-1<x<3,BC⊥AC垂足为点C;
①当x=0时,求tan∠BAC的值;
②若AB与y轴正半轴的所夹锐角为α,当点C在什么位置时tanα的值最大?
【答案】⑴B(-1,1)或B(-1,7)⑵①![]() ②当C(1,0)时,tanα有最大值
②当C(1,0)时,tanα有最大值![]()
【解析】试题分析:(1)在Rt△ABE中,根据勾股定理得到![]() ,得到结论;
,得到结论;
(2)①由C(x,0),当x=0时,点C与O重合,如图,设直线x=-1与x轴交于G点,过A作AF⊥x轴,通过△AOF∽△OBG可得结果;
②设直线x=-1与x轴交于H,且AF⊥X
于F,根据平行线的性质得到∠ABH=α由三角形函数得到tanα=![]() ,根据相似三角形的性质可得
,根据相似三角形的性质可得![]() ,于是得到二次函数,配方后根据二次函数的性质可求解.
,于是得到二次函数,配方后根据二次函数的性质可求解.
试题解析:⑴如图,在Rt△ABE中(4-y)2+42=52;
解得y=1或7 ∴B(-1,1)或B(-1,7)
⑵①易证△AOF∽△OBG
∴BO:AO=OG:AF=1:4 ∴tan∠BAC(或者tan∠BAO)=![]()
②由平行可知:∠ABH=α,在Rt△ABE中tanα=![]() ,
,
∵ tanα随BH的增大而减小,∴当BH最小时tanα有最大值;即BG最大时,tanα有最大值。
易证△ACF∽△CBG 得BG/CF=CG/AF y/x-3=x+1/4
y=-![]() (x+1)(3-x)=-
(x+1)(3-x)=-![]() (x-1)2+1
(x-1)2+1
当x=1时,ymax=1 当C(1,0)时,tanα有最大值![]()

练习册系列答案
相关题目