题目内容
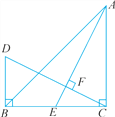
【题目】如图,点P,M,N分别在等边△ABC的各边上,且MP⊥AB,MN⊥BC,PN⊥AC.
(1)求证:△PMN是等边三角形;
(2)若AB=9 cm,求CM的长度.
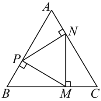
【答案】(1)见解析;(2)CM=3cm
【解析】
(1)根据等边三角形的性质得出∠A=∠B=∠C,进而得出∠MPB=∠NMC=∠PNA=90°,再根据平角的意义即可得出∠NPM=∠PMN=∠MNP,即可证得△PMN是等边三角形;
(2)易证得△PBM≌△MCN≌△NAP,得出PA=BM=CN,PB=MC=AN,从而求得BM+PB=AB=9cm,根据直角三角形30°角所对的直角边等于斜边的一半得出2PB=BM,即可求得PB的长,进而得出CM的长.
解:(1)∵△ABC是正三角形,
∴∠A=∠B=∠C,
∵MP⊥AB,MN⊥BC,PN⊥AC,
∴∠MPB=∠NMC=∠PNA=90°,
∴∠PMB=∠MNC=∠APN,
∴∠NPM=∠PMN=∠MNP,
∴△PMN是等边三角形;
(2)根据题意△PBM≌△MCN≌△NAP,
∴PA=BM=CN,PB=MC=AN,
∴BM+PB=AB=9cm,
∵△ABC是正三角形,
∴∠A=∠B=∠C=60°,
∴2PB=BM,
∴2PB+PB=9cm,
∴PB=3cm,
∴CM=3cm.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目