题目内容
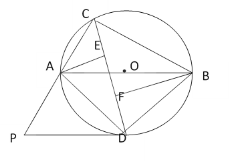
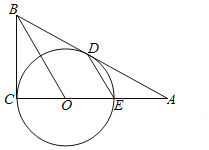
【题目】如图,在![]() 是AC上的一点,
是AC上的一点,![]() 与
与![]() 分别切于点
分别切于点![]() ,与AC相交于点E,连接BO.
,与AC相交于点E,连接BO.
![]() 求证:
求证:![]()
![]() 若
若![]() ,则
,则![]() ______,
______,![]() ______;
______;
【答案】2;4
【解析】试题分析:(1)证明△BCO∽△CDE,得![]() ,并将CO=
,并将CO=![]() CE代入,可得:CE2=2DEBO;
CE代入,可得:CE2=2DEBO;
(2)连接OD,设AE=x,则AO=x+3,AC=x+6.根据△ODA∽△BCA,![]() ,列方程可得x的值.在Rt△ADO中 由勾股定理可得AD的值.
,列方程可得x的值.在Rt△ADO中 由勾股定理可得AD的值.
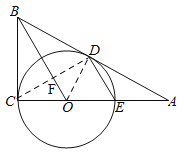
试题解析:(1)证明:连接CD,交OB于F.∵BC与⊙O相切于C,∴∠BCO=90°.
∵EC为⊙O的直径,∴∠CDE=90°,∴∠BCO=∠CDE.
∵BC、BC分别与⊙O相切于C,D,∴BC=BD.
∵OC=OD,∴BO垂直平分CD,从而在Rt△BCO中,CF⊥BO得:∠CBO=∠DCE,
故△BCO∽△CDE,得![]() ,∴CECO=BODE.
,∴CECO=BODE.
又∵CO=![]() CE,∴CE2=2DEBO;
CE,∴CE2=2DEBO;
(2)连接OD.∵BC=CE=6,OD=OE=OC=3,设AE=x,则AO=x+3,AC=x+6.
由△ODA∽△BCA,![]() ,∴
,∴![]() ,得:AB=2(x+3).
,得:AB=2(x+3).
在Rt△ABC 由勾股定理得:62+(x+6)2=(2x+6)2,解得:x1=2.x2=﹣6(舍)
∴AE=2,∴AO=OE+AE=3+2=5.
从而在Rt△ADO中 由勾股定理解得:AD=4.
故答案为:2,4.

练习册系列答案
相关题目