题目内容
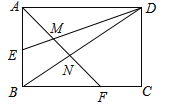
【题目】如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
过F作FH⊥AD于H,交ED于O,于是得到FH=AB=2,根据勾股定理得到AF=![]() =
=![]() =
=![]() ,根据平行线分线段成比例定理得到,OH=
,根据平行线分线段成比例定理得到,OH=![]() AE=
AE=![]() ,由相似三角形的性质得到
,由相似三角形的性质得到![]() =
=![]() ,求得AM=
,求得AM=![]() AF=
AF=![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() =
=![]() ,求得AN=
,求得AN=![]() AF=
AF=![]() ,即可得到结论.
,即可得到结论.
过F作FH⊥AD于H,交ED于O,则FH=AB=2.
∵BF=2FC,BC=AD=3,
∴BF=AH=2,FC=HD=1,
∴AF=![]() =
=![]() =
=![]() ,
,
∵OH∥AE,
∴![]() =
=![]() ,
,
∴OH=![]() AE=
AE=![]() ,
,
∴OF=FH﹣OH=2﹣![]() =
=![]() ,
,
∵AE∥FO,∴△AME∽△FMO,
∴![]() =
=![]() ,∴AM=
,∴AM=![]() AF=
AF=![]() ,
,
∵AD∥BF,∴△AND∽△FNB,
∴![]() =
=![]() ,
,
∴AN=![]() AF=
AF=![]() ,
,
∴MN=AN﹣AM=![]() ﹣
﹣![]() =
=![]() ,故选B.
,故选B.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
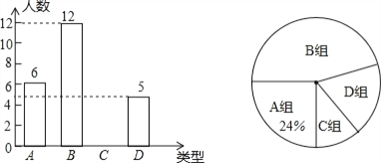
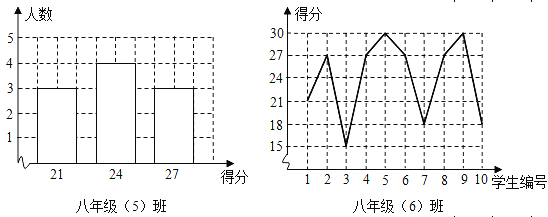
【题目】王老师为了了解学生在数学学习中的纠错情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的八年级(5)班和八年级(6)班进行了检测.并从两班各随机抽取10名学生的得分绘制成下列两个统计图.根据以上信息,整理分析数据如下:
班级 | 平均分(分) | 中位数(分) | 众数(分) |
八年级(5)班 | a | 24 | 24 |
八年级(6)班 | 24 | b | c |
(1)求出表格中a,b,c的值;
(2)你认为哪个班的学生纠错得分情况比较整齐一些,通过计算说明理由.