题目内容
【题目】如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点B出发沿线段BC、CD以2cm/s的速度向终点D运动;同时,点Q从点C出发沿线段CD、DA以1cm/s的速度向终点A运动(P、Q两点中,只要有一点到达终点,则另一点运动立即停止).
(1)运动停止后,哪一点先到终点?另一点离终点还有多远?
(2)在运动过程中,△APQ的面积能否等于22cm2?若能,需运动多长时间?若不能,请说明理由.
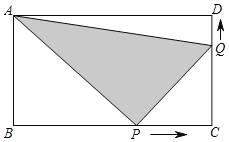
【答案】(1)点P先到终点,此时点Q离终点的距离是9cm;(2)能,需运动7s,△APQ的面积能等于22cm2.
【解析】
(1)根据题意可以分别计算出两个点运动到终点的时间,从而可以解答本题;
(2)先判断,然后计算出相应的时间即可解答本题.
(1)点P从开始到运动停止用的时间为:(12+6)÷2=9s,
点Q从开始到运动停止用的时间为:(6+12)÷1=18s.
∵9<18,只要有一点到达终点,则另一点运动立即停止,
∴点P先到终点,此时点Q离终点的距离是:(6+12)﹣1×9=9cm,
答:点P先到终点,此时点Q离终点的距离是9cm;
(2)在运动过程中,△APQ的面积能等于22cm2,
当P从点B运动到点C的过程中,设点P运动时间为as.
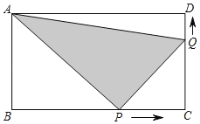
∵△APQ的面积能否等于22cm2,
![]() ,
,
∴12×6![]() 22,
22,
解得:此方程无解;
当点P从C到D的过程中,设点P运动的时间为(b+6)s.
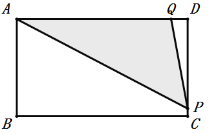
∵△APQ的面积能否等于22cm2,
![]() ,
,
∴12×6![]() 22,
22,
解得:b1=1,b2=14(舍去),
即需运动6+1=7s,△APQ的面积能等于22cm2.

练习册系列答案
相关题目