��Ŀ����
����Ŀ����2017��������21�⣩ij������ħ����������������ع�600��ħ�������߲μӣ����δ������ֽ���3��3��ħ��������ί�������������ƽ���ֵ�20������ÿ������30��ͬʱ���б��������ʱ��С��8��İ����߽�����һ�ֽ�����ͼ��3��3��ħ����A����30�����������ʱ��ͳ��ͼ����
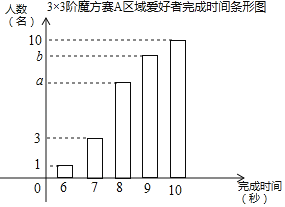
��A����3��3��ħ�������߽�����һ�ֽ���������ı������������������ʾ����
����3��3��ħ��������������������һ�£������A�����ͳ�ƽ��������3��3��ħ�����������һ�ֽ����������
����3��3��ħ����A���������ʱ���ƽ��ֵΪ8.8�룬�����Ŀ�����������ʱ��Ϊ8��İ����ߵĸ��ʣ��������������ʾ����
���𰸡���A��������һ�ֽ������������Ϊ�� ![]() ���ڹ��ƽ�����һ�ֽ��������Ϊ80�ˣ�
���ڹ��ƽ�����һ�ֽ��������Ϊ80�ˣ�
�������ʱ��Ϊ8��İ����ߵĸ���Ϊ![]() ��
��
����������������ͼ֪1��6�룬3��7�룬С��8��İ����߹���4�ˣ�������һ�ֽ������������Ϊ4��30������Ϊ���������������һ�£����Խ�����һ�ֵ�����Ϊ��600��A��������һ�ֽ���������������������ʱ���ƽ��ֵ��A��30�ˣ��õ�����a��b�Ķ�Ԫһ�η����飬���a��b���õ����ʱ��8��İ����ߵĸ��ʣ�
�����������A��С��8��Ĺ���3+1=4���ˣ�
����A��������һ�ֽ������������Ϊ��![]() ��
��
�����ƽ�����һ�ֽ��������Ϊ600��![]() =80���ˣ���
=80���ˣ���
����ΪA���������ʱ���ƽ��ֵΪ8.8�룬
���ԣ�1��6+3��7+a��8+b��9+10��10����30=8.8
����8a+9b=137������1+3+a+b+10=30����a+b=16
����![]() ,���a=7��b=9
,���a=7��b=9
���Ը������ʱ��Ϊ8��İ����ߵĸ���Ϊ![]() ��
��

 ���ʿ��ÿ��ֳɳ�ϵ�д�
���ʿ��ÿ��ֳɳ�ϵ�д�