题目内容
【题目】某童装店到厂家选购A、B两种服装.若购进A种服装12件、B种服装8件,需要资金1880元;若购进A种服装9件、B种服装10件,需要资金1810元.
(1)求A、B两种服装的进价分别为多少元?
(2)销售一件A服装可获利18元,销售一件B服装可获利30元.根据市场需求,服装店决定:购进A种服装的数量要比购进B种服装的数量的2倍还多4件,且A种服装购进数量不超过28件,并使这批服装全部销售完毕后的总获利不少于699元.设购进B种服装x件,那么:
①请写出A、B两种服装全部销售完毕后的总获利y元与x件之间的函数关系式;
②请问该服装店有几种满足条件的进货方案?哪种方案获利最多?
【答案】(1)A种型号服装每件90元,B种型号服装每件100元;(2)①y=66x+72;②有三种进货方案:B型服装购进10件,A型服装购进24件;B型服装购进11件,A型服装购进26件;B型服装购进12件,A型服装购进28件
【解析】
(1)根据题意可知,本题中的相等关系是“A种型号服装9件,B种型号服装10件,需要1810元”和“A种型号服装12件,B种型号服装8件,需要1880元”,列方程组求解即可;
(2)①若设购进B种服装x件,则购进A种服装的数量是2x+4,则y=30x+(2x+4)×18;
②利用两个不等关系列不等式组,结合实际意义求解.
解:(1)设A种型号服装每件x元,B种型号服装每件y元.依题意可得:
![]() ,
,
解得![]() ,
,
答:A种型号服装每件90元,B种型号服装每件100元.
(2)①设购进B种服装x件,则购进A种服装的数量是2x+4,
∴y=30x+(2x+4)×18,
=66x+72;
②设B型服装购进m件,则A型服装购进(2m+4)件,根据题意得:
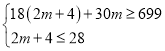 ,
,
解不等式得9![]() ≤m≤12,
≤m≤12,
因为m这是正整数,
所以m=10,11,12
2m+4=24,26,28
答:有三种进货方案:B型服装购进10件,A型服装购进24件;B型服装购进11件,A型服装购进26件;B型服装购进12件,A型服装购进28件.

 名校课堂系列答案
名校课堂系列答案【题目】为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛. 赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
分数段(分数为x分) | 频数 | 百分比 |
60≤x<70 | 8 | 20% |
70≤x<80 | a | 30% |
80≤x<90 | 16 | b% |
90≤x<100 | 4 | 10% |
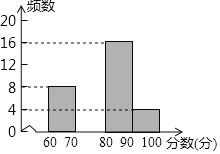
请根据图表提供的信息,解答下列问题:
(1)表中的a= ,b= ;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是 ;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学. 学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为 .