题目内容
【题目】矩形ABCD中,AB=2,AD=3,O为边AD上一点,以O为圆心,OA为半径r作⊙O,过点B作⊙O的切线BF,F为切点.
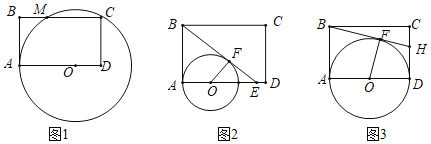
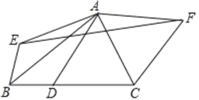
(1)如图1,当⊙O经过点C时,求⊙O截边BC所得弦MC的长度;
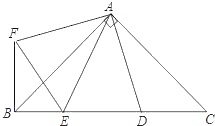
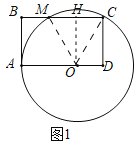
(2)如图2,切线BF与边AD相交于点E,当FE=FO时,求r的值;
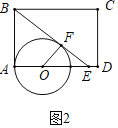
(3)如图3,当⊙O与边CD相切时,切线BF与边CD相交于点H,设△BCH、四边形HFOD、四边形FOAB的面积分别为S1、S2、S3,求![]() 的值.
的值.
【答案】(1)CM=![]() ;(2)r=2
;(2)r=2![]() ﹣2;(3)1.
﹣2;(3)1.
【解析】
(1)如图1中,连接OM,OC,作OH⊥BC于H.首先证明CM=2OD,设AO=CO=r,在Rt△CDO中,根据OC2=CD2+OD2,构建方程求出r即可解决问题.
(2)证明△OEF,△ABE都是等腰直角三角形,设OA=OF=EF=r,则OE=![]() r,根据AE=2,构建方程即可解决问题.
r,根据AE=2,构建方程即可解决问题.
(3)分别求出S1、S2、S3的值即可解决问题.
解:(1)如图1中,连接OM,OC,作OH⊥BC于H.
∵OH⊥CM,
∴MH=CH,∠OHC=90°,
∵四边形ABCD是矩形,
∴∠D=∠HCD=90°,
∴四边形CDOH是矩形,
∴CH=OD,CM=2OD,
设AO=CO=r,
在Rt△CDO中,∵OC2=CD2+OD2,
∴r2=22+(3﹣r)2,
∴r=![]() ,
,
∴OD=3﹣r=![]() ,
,
∴CM=2OD=![]() .
.
(2)如图2中,
∵BE是⊙O的切线,
∴OF⊥BE,
∵EF=FO,
∴∠FEO=45°,
∵∠BAE=90°,
∴∠ABE=∠AEB=45°,
∴AB=BE=2,
设OA=OF=EF=r,则OE=![]() r,
r,
∴r+![]() r=2,
r=2,
∴r=2![]() ﹣2.
﹣2.
(3)如图3中,
由题意:直线AB,直线BH,直线CD都是⊙O的切线,
∴BA=BF=2,FH=HD,设FH=HD=x,
在Rt△BCH中,∵BH2=BC2+CH2,
∴(2+x)2=32+(2﹣x)2,
∴x=![]() ,
,
∴CH=![]() ,
,
∴S1=![]()
S2=![]() ,
,
S3=![]() =3,
=3,
∴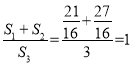 .
.

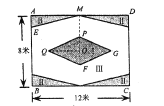
【题目】如图,某校准备给长12米,宽8米的矩形![]() 室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形
室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形![]() ),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点
),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点![]() 为矩形和菱形的对称中心,
为矩形和菱形的对称中心,![]() ,
,![]() ,
,![]() ,为了美观,要求区域Ⅱ的面积不超过矩形
,为了美观,要求区域Ⅱ的面积不超过矩形![]() 面积的
面积的![]() ,若设
,若设![]() 米.
米.
甲 | 乙 | 丙 | |
单价(元/米2) |
|
|
|
(1)当![]() 时,求区域Ⅱ的面积.
时,求区域Ⅱ的面积.
(2)计划在区域Ⅰ,Ⅱ分别铺设甲,乙两款不同的深色瓷砖,区域Ⅲ铺设丙款白色瓷砖,
①在相同光照条件下,当场地内白色区域的面积越大,室内光线亮度越好.当![]() 为多少时,室内光线亮度最好,并求此时白色区域的面积.
为多少时,室内光线亮度最好,并求此时白色区域的面积.
②三种瓷砖的单价列表如下,![]() 均为正整数,若当
均为正整数,若当![]() 米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时
米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时![]() __________,
__________,