题目内容
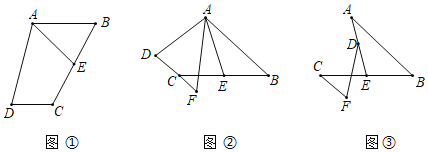
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A,B重合),BE⊥CD于E,交直线AC于F.
(1)点D在边AB上时,试探究线段BD,AB和AF的数量关系,并证明你的结论;
(2)点D在AB的延长线上时,试探究线段BD,AB和AF的数量关系,并证明你的结论.

【答案】(1)AB=FA+BD,证明详见解析;(2)点D在AB的延长线上时,AB=AF﹣BD,理由详见解析;点D在AB的反向延长线上时,AB= BD-AF,理由见解析.
【解析】
(1)由余角的性质可证∠FBA=∠FCE,根据“ASA”证明△FAB≌△DAC,可得FA=DA,从而可得到AB=AD+BD=FA+BD;
(2)分两种情况求解:①点D在AB的延长线上时,②点D在AB的反向延长线上时,画出图形并借鉴(1)中的证明思路就可解决问题.
解:(1)AB=FA+BD.
证明:如图1,
∵BE⊥CD即∠BEC=90°,∠BAC=90°,
∴∠F+∠FBA=90°,∠F+∠FCE=90°.
∴∠FBA=∠FCE.
∵∠FAB=180°﹣∠DAC=90°,
∴∠FAB=∠DAC.
在△FAB和△DAC中,
 .
.
∴△FAB≌△DAC(ASA).
∴FA=DA.
∴AB=AD+BD=FA+BD.
(2)点D在AB的延长线上时,AB=AF﹣BD,
理由如下:
①当点D在AB的延长线上时,如图2.

与(1)同样的方法可证:FA=DA,
则AB=AD﹣BD=AF﹣BD.
②点D在AB的反向延长线上时,如图3,

同理可证:FA=DA,
则AB=BD-AD=BD-AF.

 目标测试系列答案
目标测试系列答案【题目】某学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制作了不完整的统计图表.
学生借阅图书的次数统计表
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 6 | 15 | a | 12 | 9 |
学生借阅图书的次数扇形统计图

请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= ;
(2)该样本数据的中位数是 次,众数是 次;
(3)请计算扇形统计图中“3次”所对应的扇形圆心角的度数;
(4)若该校共有2400名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.