��Ŀ����
����Ŀ����1������̽������ͼ�������ı���ABCD�У�AB��CD��E��BC���е㣬AE�ǡ�BAD��ƽ���ߣ����߶�AB��AD��DC֮��ĵ�����ϵΪ�� ����
��2������Ǩ�ƣ���ͼ�������ı���ABCD�У�AB��CD��AF��DC���ӳ��߽��ڵ�F��E��BC���е㣬AE�ǡ�BAF��ƽ���ߣ���̽���߶�AB��AF��CF֮��ĵ�����ϵ����֤����Ľ��ۣ�
��3��������չ����ͼ����AB��CF��E��BC���е㣬��D���߶�AE�ϣ���EDF����BAE����̽���߶�AB��DF��CF֮���������ϵ����֤����Ľ��ۣ�
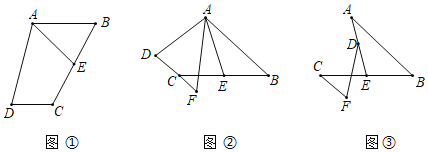
���𰸡���1��AD��AB+DC����2��AB��AF+CF��֤�������������3��AB��DF+CF��֤�����������
��������
��1�����ۣ�AD��AB+DC���ӳ�AE��DC���ڵ�F��֤����ABE�ա�FEC��AAS���������Ƴ�AB��CF����֤��DA��DF�����ɽ�����⣮
��2�����ۣ�AB��AF+CF����ͼ�����ӳ�AE��DF���ӳ����ڵ�G��֤���������ƣ�1����
��3�����ۣ�AB��DF+CF����ͼ�����ӳ�AE��CF���ӳ����ڵ�G��֤���������ƣ�1����
�⣺��1��̽�����⣺���ۣ�AD��AB+DC��
���ɣ���ͼ���У��ӳ�AE��DC���ڵ�F��

��AB��CD��
���BAF����F��
����ABE����FCE��
CE��BE����BAF����F����AEB����FEC��
���ABE�ա�FEC��AAS����
��CF��AB��
��AE����BAD��ƽ���ߣ�
���BAF����FAD��
���FAD����F��
��AD��DF��
��DC+CF��DF��
��DC+AB��AD��
�ʴ�ΪAD��AB+DC��
��2������Ǩ�ƣ����ۣ�AB��AF+CF��
֤������ͼ�����ӳ�AE��DF���ӳ����ڵ�G��

��E��BC���е㣬
��CE��BE��
��AB��DC��
���BAE����G����BE��CE����AEB����GEC
���AEB�ա�GEC��AAS��
��AB��GC
��AE����BAF��ƽ����
���BAG����FAG��
�ߡ�BAG��G��
���FAG����G��
��FA��FG��
��CG��CF+FG��
��AB��AF+CF��
��3��������չ�����ۣ�AB��DF+CF��
֤������ͼ�����ӳ�AE��CF���ӳ����ڵ�G��

��E��BC���е㣬
��CE��BE��
��AB��CF��
���BAE����G��
����AEB����GEC��
 ��
��
���AEB�ա�GEC��
��AB��GC��
�ߡ�EDF����BAE��
���FDG����G��
��FD��FG��
��AB��DF+CF��

 ״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�