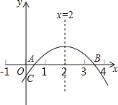题目内容
【题目】如图,在平面直角坐标系中,直线y=﹣x+2交x轴于点A,交y轴于点B,过点A的抛物线y=ax2+bx﹣2与y轴交点C,与直线AB的另一个交点为D,点E是线段AD上一点,点F在抛物线上,EF∥y轴,设E的横坐标为m
(1)用含a的代数式表示b.
(2)当点D的横坐标为8时,求出a的值.
(3)在(2)的条件下,设△ABF的面积为S,求出S最大值,并求出此时m的值.
【答案】(1) b=1﹣2a;(2)a=﹣![]() ;(3)m=5时,△ABF的面积最大,最大值为
;(3)m=5时,△ABF的面积最大,最大值为![]() .
.
【解析】
(1)把A(2,0)代入y=ax2+bx﹣2得到4a+2b﹣2=0,即可得b=1﹣2a;(2)先求得点D的坐标为(8,﹣6),代入y=ax2+bx﹣2中,结合(1)即可求得a的值;(3)如图,连接AF、BF,作FH⊥AB用H.设E(m,﹣m+2),则F(m,﹣![]() m+
m+![]() m﹣2),构建△ABF的面积为S与m的二次函数关系,利用二次函数的性质解答即可.
m﹣2),构建△ABF的面积为S与m的二次函数关系,利用二次函数的性质解答即可.
(1)由题意A(2,0),B(0,2),
把A(2,0)代入y=ax2+bx﹣2得到4a+2b﹣2=0,
∴b=1﹣2a.
(2)∵D的横坐标为8,
x=8时,y=﹣8+2=﹣6,
∴D(8,﹣6),
把D(8,﹣6)代入y=ax2+bx﹣2得到:64a+8b﹣2=﹣6,
∴64a+8(1﹣2a)﹣2=﹣6,
∴a=﹣![]() .
.
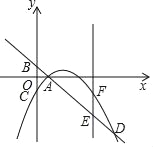
(3)如图,连接AF、BF,作FH⊥AB用H.设E(m,﹣m+2),则F(m,﹣![]() m+
m+![]() m﹣2).
m﹣2).

∵OA=OB=2,∠AOB=90°,
∴∠ABO=45°,AB=2![]() ,
,
∵EF∥OB,
∴∠FEH=∠OBA=45°,
∴FH=![]() EF,
EF,
∴S△ABF=![]() ×AB×FH=
×AB×FH=![]() ×2
×2![]() ×
×![]() (﹣
(﹣![]() m2+
m2+![]() m﹣4)=﹣
m﹣4)=﹣![]() (m﹣5)2+
(m﹣5)2+![]() ,
,
∵﹣![]() <0,
<0,
∴m=5时,△ABF的面积最大,最大值为![]() .
.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案【题目】一蓄水池有水40m3,按一定的速度放水,水池里的水量y (m3)与放水时间t(分)有如下关系:
放水时间(分) | 1 | 2 | 3 | 4 | ... |
水池中水量(m) | 38 | 36 | 34 | 32 | ... |
下列结论中正确的是
A. y随t的增加而增大B. 放水时间为15分钟时,水池中水量为8m3
C. 每分钟的放水量是2m3D. y与t之间的关系式为y=38-2t