题目内容
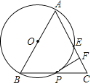
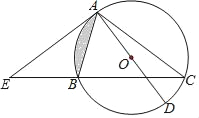
【题目】如图,△ABC内接于⊙O,AD是⊙O直径,E是CB延长线上一点,且∠BAE=∠C.
(1)求证:直线AE是⊙O的切线;
(2)若∠BAE=30°,⊙O的半径为2,求阴影部分的面积;
(3)若EB=AB,cos∠E=![]() ,AE=24,求EB的长及⊙O的半径.
,AE=24,求EB的长及⊙O的半径.
【答案】(1)见解析;(2) ![]() π﹣
π﹣![]() ;(3)BE=20,半径:
;(3)BE=20,半径:![]() .
.
【解析】
(1)连接BD,利用圆周角定理得到∠ABD=90°,则∠D+∠DAB=90°,再利用等量代换证明∠DAE=90°,然后根据切线的判定定理即可得到结论;
(2)连接OB,先计算出∠OAB=60°,得到△AOB为等边三角形,所以∠AOB=60°,然后利用阴影部份的面积=S扇形AOB﹣S△AOB进行计算;
(3)作BH⊥AE于H,利用等腰三角形的性质得AH=EH=![]() AE=12,∠E=∠BAE.在Rt△BEH中利用余弦的定义可计算出BE=20,则AB=20,由于∠D=∠C=∠BAE=∠E,则cos∠D=
AE=12,∠E=∠BAE.在Rt△BEH中利用余弦的定义可计算出BE=20,则AB=20,由于∠D=∠C=∠BAE=∠E,则cos∠D=![]() .在Rt△ABD中,cos∠D=
.在Rt△ABD中,cos∠D=![]() =
=![]() ,设BD=3x,AD=5x,易得4x=20,解出x得到AD的长,从而得到⊙O的半径.
,设BD=3x,AD=5x,易得4x=20,解出x得到AD的长,从而得到⊙O的半径.
(1)连接BD,如图,∵AD为直径,∴∠ABD=90°,∴∠D+∠DAB=90°.
∵∠C=∠D,∠BAE=∠C,∴∠BAE+∠DAB=90°,即∠DAE=90°,∴AD⊥AE,∴直线AE是⊙O的切线;
(2)连接OB,如图,∵∠BAE=30°,∴∠OAB=60°,而OA=OB,∴△AOB为等边三角形,∴∠AOB=60°,∴阴影部份的面积=S扇形AOB﹣S△AOB=![]() ﹣
﹣![]() ×22=
×22=![]() π﹣
π﹣![]() ;
;
(3)作BH⊥AE于H,如图,∵EB=AB,∴AH=EH=![]() AE=12,∠E=∠BAE.在Rt△BEH中,∵cos∠E=
AE=12,∠E=∠BAE.在Rt△BEH中,∵cos∠E=![]() =
=![]() ,∴BE=12×
,∴BE=12×![]() =20,∴AB=BE=20.
=20,∴AB=BE=20.
∵∠D=∠C=∠BAE=∠E,∴cos∠D=![]() .在Rt△ABD中,cos∠D=
.在Rt△ABD中,cos∠D=![]() =
=![]() ,设BD=3x,AD=5x,∴AB=4x,即4x=20,解得:x=5,∴AD=25,∴⊙O的半径为
,设BD=3x,AD=5x,∴AB=4x,即4x=20,解得:x=5,∴AD=25,∴⊙O的半径为![]() .
.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
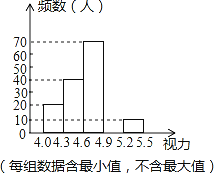
初中暑期衔接系列答案【题目】某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)在频数分布表中,a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?