题目内容
【题目】某公司随机选取40名员工进行普法知识考查,对考查成绩进行统计(成绩均为整数,满分100分),并依据统计数据绘制了如下尚不完整的统计表.解答下列问题:
(1) 表中a=__________,b=__________,c=__________
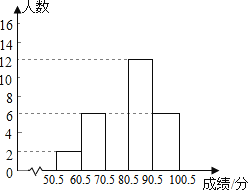
(2) 请补全频数分布直方图;
组别 | 分数段/分 | 频数/人数 | 频率 |
1 | 50.5~60.5 | 2 | a |
2 | 60.5~70.5 | 6 | 0.15 |
3 | 70.5~80.5 | b | c |
4 | 80.5~90.5 | 12 | 0.30 |
5 | 90.5~100.5 | 6 | 0.15 |
合计 | 40 | 1.00 | |
(3) 该公司共有员工3000人,若考查成绩80分以上(不含80分)为优秀,试估计该公司员工“六五”普法知识知晓程度达到优秀的人数.
【答案】 0.05 14 0.35
【解析】分析:(1)根据频率的计算公式:频率=频数![]() 总数即可求出
总数即可求出![]() ;利用总数40减去其它各组的频数求得b,
;利用总数40减去其它各组的频数求得b,
(2)根据![]() 即可作出直方图;
即可作出直方图;
(3)利用总数3000乘以最后两组的频率的和即可求解.
详解:(1)a=![]() =0.05,
=0.05,
第三组的频数b=40-2-6-12-6=14,
频率c=![]() =0.35;
=0.35;
(2)补全频数分布直方图如下: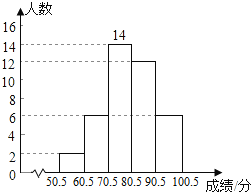 ;
;
(3)3000×(0.30+0.15)=1350(人).
答:该公司员工“六五”普法知识知晓程度达到优秀的人数1350人.

【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品 | B种产品 | |
成本(万元/件) | 2 | 5 |
利润(万元/件) | 1 | 3 |
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
【题目】甲乙两位同学参加数学综合素质测试,各项成绩如下表:(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 93 | 93 | 89 | 90 |
学生乙 | 94 | 92 | 94 | 86 |
(1)分别计算甲、乙同学成绩的中位数;
(2)如果数与代数,空间与图形,统计与概率,综合与实践的成绩按4:3:1:2计算,那么甲、乙同学的数学综合素质成绩分别为多少分?