题目内容
【题目】如图，在平面直角坐标系中，四边形OABC是矩形，其中点A在x轴的正半轴上，点B的坐标为（4，2），点D为对角线OB上一个动点（不包括端点），∠BCD的平分线交OB于点E．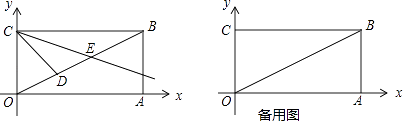
（1）求线段OB所在直线的函数表达式，并写出CD的取值范围．
（2）当∠BCD的平分线经过点A时，求点D的坐标．
（3）点P是线段BC上的一个动点，求CD十DP的最小值．
【答案】
（1）
解：设线段OB所在直线的函数表达式为y=kx，
把B（4，2）代入，得2=4k，解得k= 
，
∴线段OB所在直线的函数表达式为y= x．
CD的范围： 
≤CD＜4
（2）
解：如图1中，延长CD交OA于点F，
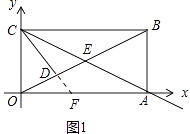
∵∠ACF=∠ACB=∠CAF，
∴AF=CF，设AF=CF=m，则OF=4﹣m，
∵OF2+OC2=CF2，
∴（4﹣m）2+22=m2，解得m= 
，
∴直线CF的解析式为y=﹣ 
x+2，
由 
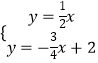解得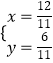 
，
∴点D坐标（ 
， 
）
（3）
解：如图2中，作点C关于直线OB的对称点F，作FP⊥BC，交OB于D，垂足为P，则点P、D就是所求的点，此时DC+DP=DF+PD=FP最短（垂线段最短）．
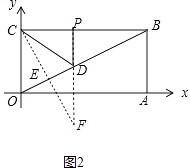
设直线CF的解析式为y=﹣2x+b，把C（0，2）代入得b=2，
∴直线CF解析式为y=﹣2x+2，设直线CF交OB于点E，
由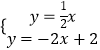 
解得 
，
∴点E坐标（ 
， 
），
∵C、F关于点E对称，
∴点F坐标（ 
，﹣ 
），
∴CD+PD最小值=PF=2+ = 
【解析】（1）设线段OB所在直线的函数表达式为y=kx，把B（4，2）代入求出k即可解决问题．（2）如图1中，延长CD交OA于点F，设AF=CF=m，则OF=4﹣m，由OF2+OC2=CF2 ， 列出方程求出m，求出直线CF的解析式，解方程组即可解决问题．（3）如图2中，作点C关于直线OB的对称点F，作FP⊥BC，交OB于D，垂足为P，则点P、D就是所求的点，此时DC+DP=DF+PD=FP最短，求出点F坐标即可解决问题．
【考点精析】解答此题的关键在于理解正比例函数的图象和性质的相关知识，掌握正比函数图直线，经过一定过原点．K正一三负二四，变化趋势记心间．K正左低右边高，同大同小向爬山．K负左高右边低，一大另小下山峦，以及对勾股定理的概念的理解，了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
