题目内容
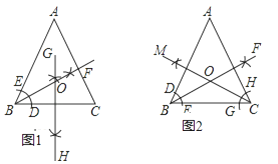
【题目】已知:△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点M是BE的中点,连接CM、DM.

(1)当点D在AB上,点E在AC上时(如图一),求证:DM=CM,DM⊥CM;
(2)当点D在CA延长线上时(如图二)(1)中结论仍然成立,请补全图形(不用证明);
(3)当ED∥AB时(如图三),上述结论仍然成立,请加以证明.
【答案】(1)证明见解析;(2)见解析;(3)见解析.
【解析】
(1)如图一中,延长![]() 使得
使得![]() ,连接
,连接![]() 、
、![]() ,先证明
,先证明![]() ,再证明
,再证明![]() 即可解决问题.
即可解决问题.
(2)补充图形如图二所示,延长![]() 交
交![]() 的延长线于
的延长线于![]() ,只要证明
,只要证明![]() ,再证明
,再证明![]() 是等腰直角三角形即可.
是等腰直角三角形即可.
(3)如图三中,如图一中,延长![]() 使得
使得![]() ,连接
,连接![]() 、
、![]() ,
,![]() ,先证明
,先证明![]() ,再证明
,再证明![]() 即可.
即可.
(1)证明:如图一中,延长DM使得MN=DM,连接BN、CN.

在△DME和△NMB中, ,
,
∴△DME≌△NMB,
∴DE=BN,∠MDE=∠MNB,
∴DE∥NB,
∴∠ADE=∠ABN=90°,
∵△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,
∴AD=DE=BN,AC=BC,∠A=∠ABC=45°,
∴∠CBN=45°=∠A,
在△ACD和△BCN中,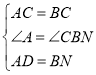 ,
,
∴△ACD≌△BCN,
∴DC=CN,∠ACD=∠BCN,
∴∠DCN=∠ACB=90°,
∴△DCN是等腰直角三角形,
DM=MN,
∴DM=CM.DM⊥CM
(2)解:如图二所示
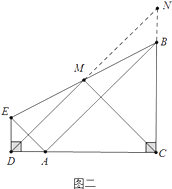
延长DM交CB的延长线于N, ∵△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,
∴AD=DE=BN,AC=BC,∠A=∠ABC=45°,
∵∠EDC+∠DCN=180°,
∴DE∥CN,
∴∠EDM=∠N
在△DME和△NMB中, ,
,
∴△DME≌△NMB,
∴DE=BN=AD,DM=MN,
∴CD=CN,
∴∠CDN=∠N=45°,CM=DM=MN,CM⊥DN,
∴DM=CM.DM⊥CM.
(3)证明:如图三中,如图一中,延长DM交AB于N连接CN.

∵DE∥AB,
∴∠MBN=∠MED,
在△DME和△NMB中,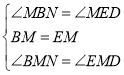 ,
,
∴△DME≌△NMB,
∴DE=BN=AD,DM=MN,
∵△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,
∴AD=DE=BN,AC=BC,∠BAC=∠ABC=45°,
∵∠AED+∠BAE=180°,
∴∠BAE=135°,
∵∠BAC=∠EAD=45°,
∴∠DAC=∠CBN=45°
在△ACD和△BCN中, ,
,
∴△ACD≌△BCN,
∴DC=CN,∠ACD=∠BCN,
∴∠DCN=∠ACB=90°,
∴△DCN是等腰直角三角形,∵DM=MN,
∴DM=CM.DM⊥CM

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案