题目内容
【题目】如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆. 
(1)求证:AB是⊙O的切线;
(2)若AC=8,tan∠BAC= ![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】
(1)解:连结OP、OA,OP交AD于E,如图,
∵PA=PD,
∴弧AP=弧DP,
∴OP⊥AD,AE=DE,
∴∠1+∠OPA=90°,
∵OP=OA,
∴∠OAP=∠OPA,
∴∠1+∠OAP=90°,
∵四边形ABCD为菱形,
∴∠1=∠2,
∴∠2+∠OAP=90°,
∴OA⊥AB,
∴直线AB与⊙O相切;
(2)解:连结BD,交AC于点F,如图,
∵四边形ABCD为菱形,
∴DB与AC互相垂直平分,
∵AC=8,tan∠BAC= ![]() ,
,
∴AF=4,tan∠DAC= ![]() =
= ![]() ,
,
∴DF=2 ![]() ,
,
∴AD= ![]() =2
=2 ![]() ,
,
∴AE= ![]() ,
,
在Rt△PAE中,tan∠1= ![]() =
= ![]() ,
,
∴PE= ![]() ,
,
设⊙O的半径为R,则OE=R﹣ ![]() ,OA=R,
,OA=R,
在Rt△OAE中,∵OA2=OE2+AE2,
∴R2=(R﹣ ![]() )2+(
)2+( ![]() )2,
)2,
∴R= ![]() ,
,
即⊙O的半径为 ![]() .
.
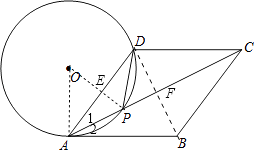
【解析】(1)连结OP、OA,OP交AD于E,由PA=PD得弧AP=弧DP,根据垂径定理的推理得OP⊥AD,AE=DE,则∠1+∠OPA=90°,而∠OAP=∠OPA,所以∠1+∠OAP=90°,再根据菱形的性质得∠1=∠2,所以∠2+∠OAP=90°,然后根据切线的判定定理得到直线AB与⊙O相切;(2)连结BD,交AC于点F,根据菱形的性质得DB与AC互相垂直平分,则AF=4,tan∠DAC= ![]() ,得到DF=2
,得到DF=2 ![]() ,根据勾股定理得到AD=
,根据勾股定理得到AD= ![]() =2
=2 ![]() ,求得AE=
,求得AE= ![]() ,设⊙O的半径为R,则OE=R﹣
,设⊙O的半径为R,则OE=R﹣ ![]() ,OA=R,根据勾股定理列方程即可得到结论.
,OA=R,根据勾股定理列方程即可得到结论.
【考点精析】本题主要考查了菱形的性质和解直角三角形的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案