Question

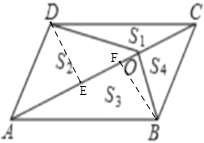
【题目】如图，在平行四边形ABCD中，点O是对角线AC上一点，连接BO、DO，△COD、△AOD、△AOB、△BOC的面积分别是S1、S2、S3、S4．下列关于S1、S2、S3、S4的等量关系式中错误的是（ ）

A.B.C.D.

Answer 1

【答案】D

【解析】

如图，分别过B、D作BF⊥AC于F，DE⊥AC于E，根据平行四边形的性质可得CD//AB，可得∠DCA=∠BAC，CD=AB，利用AAS可证明△CDE≌△ABF，可得DE=BF，根据等底等高的三角形面积相等即可得出S1=S4，S2=S3，进而对各选项逐一判断即可得答案．

如图，分别过B、D作BF⊥AC于F，DE⊥AC于E，

∵四边形ABCD是平行四边形，

∴AB=CD，AB//CD，

∴∠DCE=∠BAF，

在△CDE和△ABF中，，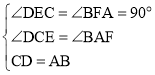

∴DE=BF，

∴OA·DE=OA·BF，OC·DE=OC·BF，即S1=S4，S2=S3，

∴S1+S3=S2+S4，，，故A、B、C选项正确，

只有OA=2OC时，S2=2S1，故D选项错误，

故选：D．