题目内容
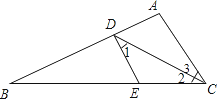
【题目】如图,在△ABC中,∠B=40°,∠C=110°.按要求完成下列各题.
(1)画出△ABC的高AD;
(2)画出△ABC的角平分线AE;
(3)根据你所画的图形求∠DAE的度数.

【答案】(1)详见解析;(2)详见解析;(3)35°.
【解析】
(1)过A点作BC延长线的垂线即可得到高AD;(2)根据角平分线的尺规作图即可作图;(3)先根据三角形的内角和求出∠CAB,再求出∠EAB,再根据三角形的外角定理求出∠AED,最后根据直角三角形求出∠DAE的度数.
(1)如图,AD即为所求作的高;

(2)如图,AE即为所求作的角平分线;
(3)在△ABC中,∵∠B=40°,∠C=110°,
∴∠CAB=180°-40°-110°=30°,
∵AE平分∠CAB,
∴∠EAB=![]() ∠CAB=15°,
∠CAB=15°,
∵∠AED是△ABE的外角,
∴∠AED=∠B+∠EAB=55°,
∵AD⊥BC,
∴∠ADB=90°,
∴在Rt△ADE中,∠DAE=90°-∠AED=90°-55°=35°.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目