Question

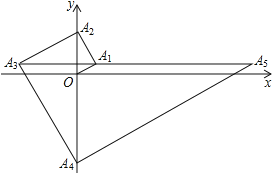
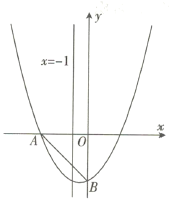
【题目】如图，对称轴为x＝1的抛物线经过A（﹣1，0），B（2，﹣3）两点．

（1）求抛物线的解析式；

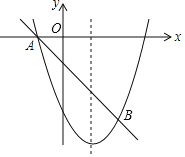
（2）P是抛物线上的动点，连接PO交直线AB于点Q，当Q是OP中点时，求点P的坐标；

（3）C在直线AB上，D在抛物线上，E在坐标平面内，以B，C，D，E为顶点的四边形为正方形，直接写出点E的坐标．

Answer 1

【答案】（1）y＝x2﹣2x﹣3；（2）点P（，）或（，）；（3）点E的坐标为：（2，﹣1）或（1，﹣4）或（0，﹣3）或（2，﹣5）.

【解析】

（1）先根据抛物线的对称性确定抛物线与x轴的另外一个交点坐标，再利用待定系数法求解即可；

（2）先利用待定系数法求出直线AB的解析式，再设出点P坐标，由Q是OP中点即可表示出点Q坐标，然后把点Q代入直线AB的解析式，解方程即可求出结果；

（3）分BC为正方形的对角线、BC是正方形的一条边两种情况，画出图形，分别根据正方形的性质求解即可．

解：（1）对称轴为x＝1的抛物线经过A（﹣1，0），则抛物线与x轴的另外一个交点坐标为：（3，0），

设抛物线的表达式为：y＝a（x+1）（x﹣3），将点B的坐标代入上式并解得：a＝1，

故抛物线的表达式为：y＝（x+1）（x﹣3）＝x2﹣2x﹣3；

（2）设直线AB的解析式为：，

将点A、B的坐标代入，得：，

解得：，

∴直线AB的表达式为：y＝﹣x﹣1，

设点P（m，m2﹣2m﹣3），当Q是OP中点时，则点Q（m，），

将点Q的坐标代入直线AB 的表达式，得，

解得：m＝，

故点P（，）或（，）；

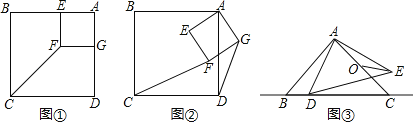
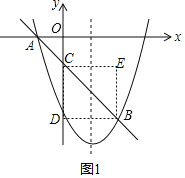
（3）①当BC为正方形的对角线时，如图1所示，

∵直线AB的表达式为：y＝﹣x﹣1，则点C（0，﹣1），点D（0，﹣3），

∴BE＝CD＝2，故点E1（2，﹣1）；

②当BC是正方形的一条边时，

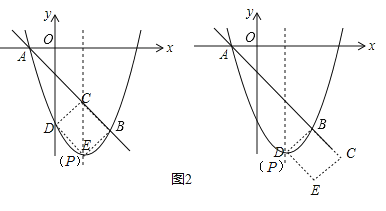
（Ⅰ）当点D在BC下方时，如图2所示，

抛物线顶点P的坐标为：（1，﹣4），点B（2，﹣3），可得PB⊥BC，

有图示两种情况，左图，点C、E的横坐标相同，在函数对称轴上，故点E2（1，﹣4）；

此时，点D、E的位置可以互换，故点E3（0，﹣3）；

右图，点B、E的横坐标相同，

∵D（1，﹣4），∴E4（2，﹣5）；

（Ⅱ）当点D在AB上方时，此时要求点B与点D横坐标相同，这是不可能的，故不存在；

综上，点E的坐标为：（2，﹣1）或（1，﹣4）或（0，﹣3）或（2，﹣5）．