Question

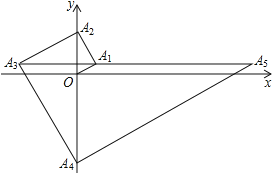
【题目】如图，在平面直角坐标系中，OA1＝2，∠A1Ox＝30°，以OA1为直角边作Rt△OA1A2，并使∠A1OA2＝60°，再以A1A2为直角边作Rt△A1A2A3，并使∠A2A1A3＝60°，再以A2A3为直角边作Rt△A2A3A4，并使∠A3A2A4＝60°，…，按此规律进行下去，则A2020的坐标是_____．

Answer 1

【答案】（0，1﹣31010）

【解析】

先根据已知确定A2在y轴正半轴上，A3在第二象限，A4在y轴负半轴上，由此可得每四个点一循环，而2020是4的倍数，所以可确定所求点在y轴的负半轴上，再根据解直角三角形的知识依次求得A2，A3，A4的坐标，找到规律即可求出答案．

解：如图，设A1A3与y轴交于点B，

∵∠A1Ox＝30°，∠A1OA2＝60°，

∴∠A2Ox＝90°，

∴A2在y轴上，

在Rt△A1A2O中，∵OA1＝2，∠A1OA2＝60°，

∴∠A1A2O＝30°，

∴OA2＝2OA1＝4，A1A2＝2，

∴A2（0，4），

在Rt△A1A2A3中，∵∠A2A1A3＝60°，

∴∠A1A3A2＝30°，

∴A1A3＝2A1A2＝4，

∵∠BA1O＝∠A1Ox＝30°，

∴A1B∥x轴，

∴A1B⊥A2O，

∵∠A1A2B＝30°，

∴A1B＝A1A2＝，A2B＝3，

∴A3B＝4﹣＝3，OB＝4﹣3＝1，

∴A3的横坐标为：﹣3＝﹣，

∴A3（﹣3，1），

在Rt△A2BA3中，A2A3＝2A2B＝6，在Rt△A2A3A4中，A2A4＝2A2A3＝12，

∴OA4＝12﹣4＝8，

∴A4的纵坐标为：，A4（0，﹣8），

由此发现：点A1，A2，A3，A4，…，An，每四次一循环，

∵2020÷4＝505，∴点A2020在y轴的负半轴上，纵坐标是：＝1﹣31010．

则A2020的坐标是 （0，1﹣31010）；

故答案为：（0，1﹣31010）．