题目内容
【题目】如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=80°,点P为⊙O上任意一点(不与E、F重合),则∠EPF=______.
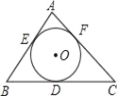
【答案】50°或130°
【解析】
有两种情况:①当P在弧EDF上时,连接OE、OF,求出∠EOF,根据圆周角定理求出即可;②当P在弧EMF上时,∠EPF=∠EMF,根据圆内接四边形的性质得到∠EMF+∠ENF=180°,代入求出即可.
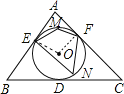
有两种情况:
①当P在弧EDF上时,∠EPF=∠ENF,连接OE、OF,
∵圆O是△ABC的内切圆,∴OE⊥AB,OF⊥AC,∴∠AEO=∠AFO=90°,
∵∠A=80°,∴∠EOF=360°∠AEO∠AFO∠A=100°,∴∠ENF=∠EPF=![]() ∠EOF=50°,
∠EOF=50°,
②当P在弧EMF上时,∠EPF=∠EMF,∠FPE=∠FME=180°50°=130°.
故答案为:50°或130°.

练习册系列答案
相关题目
【题目】已知关于x的一元二次方程x2-(2m+3)x+m2+2=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程的两个根分别为x1、x2,且满足x12+x22=31+x1x2,求实数m的值.
【题目】为庆祝新中国成立70周年,并体现绿色节能理念,我市某工厂降低了某种工艺品的成本,两个月内从每件产品成本50元,降低到了每件32元,
(1)请问工厂平均每月降低率为多少?
(2)该工厂将产品投放市场进行实销,经过调查,得到如下数据:
销售单价 | …… | 40 | 50 | 60 | 70 | …… |
每天销售量 | …… | 400 | 300 | 200 | 100 | …… |
把上表中![]() 、
、![]() 的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想![]() 与
与![]() 的函数关系,并求出函数关系式.
的函数关系,并求出函数关系式.
(3)当销售单价定为多少时,工艺厂试销该工艺品每天活得的利润最大?最大利润是多少?