Question

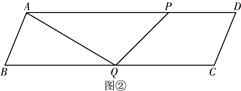
【题目】如图①，在□ABCD中，AB＝13，BC＝50，BC边上的高为12．点P从点B出发，沿B-A-D-A运动，沿B-A运动时的速度为每秒13个单位长度，沿A-D-A运动时的速度为每秒8个单位长度．点Q从点 B出发沿BC方向运动，速度为每秒5个单位长度. P、Q两点同时出发，当点Q到达点C时，P、Q两点同时停止运动．设点P的运动时间为t（秒）．连结PQ．

（1）当点P沿A-D-A运动时，求AP的长（用含t的代数式表示）．

（2） 当点P与点D重合时，求t的值

（3）连结AQ，在点P沿B-A-D运动过程中，当点P与点B、点A不重合时，记△APQ的面积为S．求S与t之间的函数关系式.

Answer 1

【答案】见解析.

【解析】整体分析：

（1）分两种情况求：当点P沿AD运动时和当点P沿DA运动时；（2）用AP=AD列方程求解；（3）画出当0＜t＜1和1＜t≤时的图形，根据三角形的面积公式求解.

（1）当点P沿AD运动时，AP＝＝.

当点P沿DA运动时，AP＝50×28＝108.

（2）当点P与点D重合时，AP＝AD， ＝50，t＝.

（3）当点P与点A重合时，BP＝AB＝1.

当点P与点D重合时，AP＝AD， ＝50，t＝.

当0＜t＜1时，如图①.

作过点Q作QE⊥AB于点E.

S△ABQ＝＝，

∴QE＝＝＝.

∴S＝.

当1＜t≤时，如图②.

S＝＝，

∴S＝.