题目内容
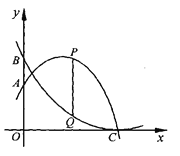
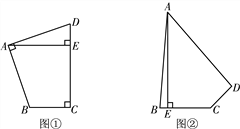
【题目】探究:如图①, 在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,AE⊥CD于点E.若AE=10,求四边形ABCD的面积.
应用:如图②,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,AE⊥BC于点E.若AE=19,BC=10,CD=6,则四边形ABCD的面积为 .
【答案】100;152.
【解析】整体分析:
探究:过点A作AF⊥CB,交CB的延长线于点F,证△AFB≌△AED,得四边形AFCE是正方形;应用,过点A作AG⊥CD的延长线于点G,连接AC,证△ABE≌△ADG,△AEC≌△AGC,求△AEC的面积,四边形ABCD的面积=四边形AECG的面积求解.
解:探究,过点A作AF⊥CB,交CB的延长线于点F.
∵AE⊥CD,∠BCD=![]() ,
,
∴四边形AFCE为矩形.
∴∠FAE=![]() .
.
∴∠FAB+∠BAE=![]() .
.
∵∠EAD+∠BAE=![]() ,
,
∴∠FAB=∠EAD.
∵AB=AD,∠F=∠AED=![]() ,
,
∴△AFB≌△AED.
∴AF=AE.
∴四边形AFCE为正方形.
∴![]() =
=![]() =
=![]() =
=![]() =100.
=100.
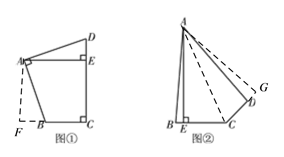
应用,过点A作AG⊥CD的延长线于点G,连接AC,
∴∠AEB=∠AGD=90°,
∵∠ABC+∠ADC=180°,∠ADC+∠ADG=180°,
∴∠ABC=∠ADG,
又∵AB=AD,
∴△ABE≌△ADG,
∴AB=AG,BE=DG,
又∵AC=AC,
∴△AEC≌△AGC,
∴CE=CG,
∴BE=BC-CE=BC-CG=BC-CD-DG=BC-CD-BE,
∵BC=10,CD=6,
∴BE=2,∴EC=10-2=8,
∴S△AEC=![]() ×CE×AE=
×CE×AE=![]() ×8×19=76.
×8×19=76.
∴四边形ABCD的面积=四边形AECG的面积=2S△AEC.
∴四边形ABCD的面积=2×76=152.

练习册系列答案
相关题目